Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 23. Đại lượng tỉ lệ nghịch trang 15 SGK Toán 7 kết nối tri thức
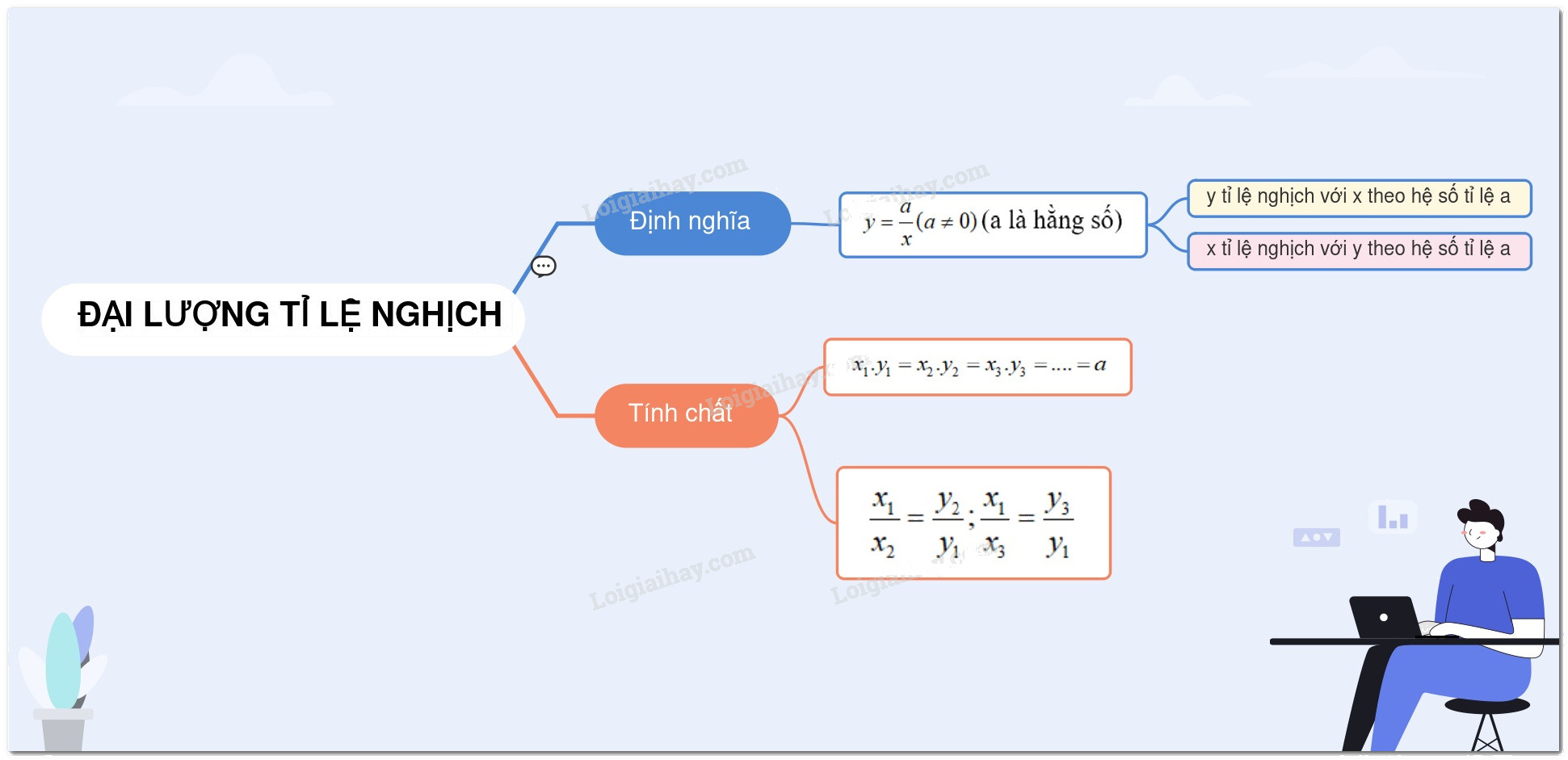
Lý thuyết Đại lượng tỉ lệ nghịch Toán 7 Kết nối tri thức
Giải mục 1 trang 15,16 SGK Toán 7 tập 2 - Kết nối tri thức Giải mục 2 trang 17, 18 SGK Toán 7 tập 2 - Kết nối tri thức Giải bài 6.22 trang 18 SGK Toán 7 tập 2 - Kết nối tri thức Giải bài 6.23 trang 18 SGK Toán 7 tập 2 - Kết nối tri thức Giải bài 6.24 trang 18 SGK Toán 7 tập 2 - Kết nối tri thức Giải bài 6.25 trang 18 SGK Toán 7 tập 2 - Kết nối tri thức Giải bài 6.26 trang 18 SGK Toán 7 tập 2 - Kết nối tri thứcLý thuyết Đại lượng tỉ lệ nghịch Toán 7 Kết nối tri thức
Định nghĩa tỉ lệ nghịch
1. Các kiến thức cần nhớ
Định nghĩa tỉ lệ nghịch
+ Nếu đại lượng liên hệ với đại lượng theo công thức hay (với là hằng số khác ) thì ta nói tỉ lệ nghịch với theo hệ số tỉ lệ
+ Khi đại lượng tỉ lệ nghịch với đại lượng thì cũng tỉ lệ nghịch với và ta nói hai đại lượng đó tỉ lệ nghịch với nhau.
Ví dụ: Nếu thì tỉ lệ nghịch với theo hệ số tỉ lệ là
Chú ý: Khi tỉ lệ nghịch với theo hệ số tỉ lệ , ta cũng nói tỉ lệ nghịch với theo hệ số tỉ lệ
Tính chất
* Nếu hai đại lượng tỉ lệ nghịch với nhau thì:
+ Tích hai giá trị tương ứng của chúng luôn luôn không đổi.
+ Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia.
* Nếu hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ thì:
2. Các dạng toán thường gặp
Dạng 1: Bảng giá trị tương ứng của hai đại lượng tỉ lệ nghịch
Phương pháp:
+ Xác định hệ số tỉ lệ
+ Dùng công thức hoặc để tìm các giá trị tương ứng của và
Dạng 2: Xét tương quan tỉ lệ nghịch giữa hai đại lượng khi biết bảng các giá trị tương ứng của chúng
Phương pháp:
Xét xem tất cả các tích các giá trị tương ứng của hai đại lượng có bằng nhau không?
Nếu bằng nhau thì hai đại lượng tỉ lệ nghịch.
Nếu không bằng nhau thì hai đại lượng không tỉ lệ nghịch.
Dạng 3: Bài toán về các đại lượng tỉ lệ nghịch
Phương pháp:
+ Xác định rõ các đại lượng có trên đề bài.
+ Xác định tương quan tỉ lệ nghịch giữa hai đại lượng.
+ Áp dụng tính chất về tỉ số các giá trị của hai đại lượng tỉ lệ nghịch và tính chất tỉ lệ thức để giải bài toán.
Dạng 4: Chia một số thành những phần tỉ lệ nghịch với các số cho trước
Phương pháp:
Giả sử chia số thành ba phần tỉ lệ nghịch với các số cho trước. Ta có
hay
Như vậy để chia số thành các phần tỉ lệ nghịch với các số (khác ), ta chỉ cần chia số thành các phần tỉ lệ thuận với các số (đã biết cách làm).
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365