Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
BÀI 11: CẢNH ĐẸP NON SÔNG
Giải Bài đọc 2: Sông Hương VBT Tiếng Việt 3 tập 2 Cánh diều
Giải Bài viết 2: Viết về cảnh đẹp non sông VBT Tiếng Việt 3 tập 2 Cánh diều Giải Bài đọc 3: Chợ nổi Cà Mau VBT Tiếng Việt 3 tập 2 Cánh diều Giải Bài đọc 4: Sự tích thành Cổ Loa VBT Tiếng Việt 3 tập 2 Cánh diều Giải Góc sáng tạo: Đố vui: Đó là cảnh đẹp nào VBT Tiếng Việt 3 tập 2 Cánh diều Giải Bài đọc 1: Trên hồ Ba Bể VBT Tiếng Việt 3 tập 2 Cánh diềuGiải Bài đọc 2: Sông Hương VBT Tiếng Việt 3 tập 2 Cánh diều
Qua đoạn 2, em hiểu vì sao dòng sông được đặt tên là sông Hương. Câu mở đầu đoạn 3 gọi sông Hương là gì. Tìm những hình ảnh minh họa cho nhận xét nói trên về vẻ đẹp của sông Hương. Gạch dưới từ ngữ chỉ những sự vật được so sánh với nhau trong mỗi câu dưới đây.
Đọc hiểu
Câu 1:
Qua đoạn 2, em hiểu vì sao dòng sông được đặt tên là sông Hương? Khoanh tròn chữ cái trước ý đúng:
a) Vì người Huế muốn dùng tên gọi ấy để thể hiện tình yêu với dòng sông quê hương.
b) Vì xưa kia, dòng nước ở đây thường thoảng lên mùi hương dìu dịu của cây thạch xương bồ.
c) Vì lúc nào dòng nước ở đây cũng thoảng lên mùi hương dìu dịu của cây thạch xương bồ.
Câu 2
Câu mở đầu đoạn 3 gọi sông Hương là gì? Viết tiếp:
Sông Hương là .............................................................
Câu 3
Tìm những hình ảnh minh họa cho nhận xét nói trên về vẻ đẹp của sông Hương. Đánh dấu √ vào ô thích hợp:
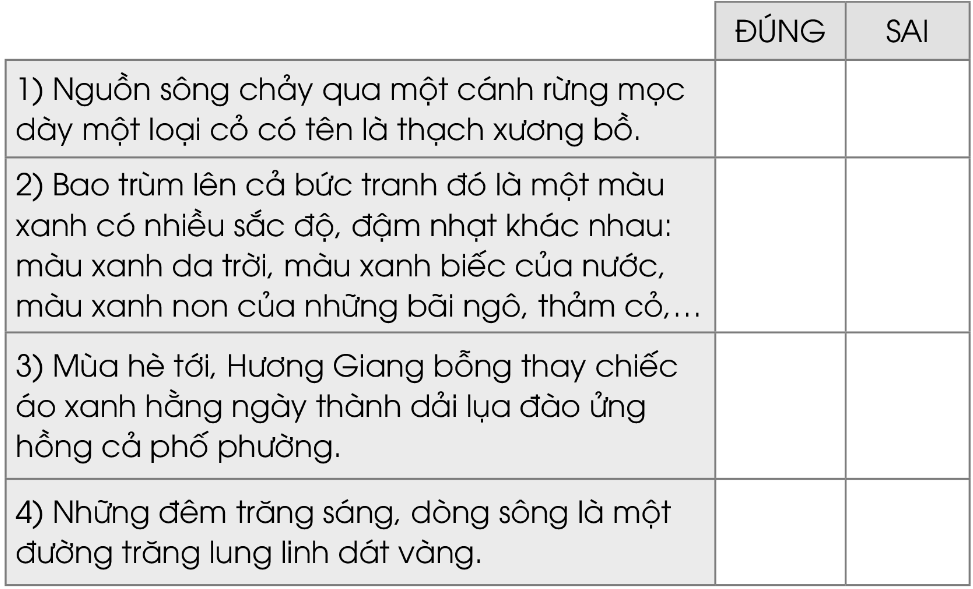
Câu 4
Gạch dưới những từ ngữ thể hiện sự thay đổi mà sông Hương tạo ra cho phố phường xung quanh:
Sông Hương là một đặc ân thiên nhiên dành cho Huế, làm cho không khí thành phố trở nên trong lành, làm tan biến những tiếng ồn ào của chợ búa, tạo cho thành phố một vẻ đẹp êm đềm.
Luyện tập
Câu 1:
Gạch dưới từ ngữ chỉ những sự vật được so sánh với nhau trong mỗi câu dưới đây:
a) Sông Hương là một bức tranh phong cảnh nhiều màu sắc.
b) Vào mùa hè, Hương Giang như một dải lụa đào.
c) Những đêm trăng sáng, dòng sông là một đường trăng dát vàng.
Câu 2
Điền từ chỉ đặc điểm thích hợp (lung linh, ửng hồng, đẹp) để thể hiện lại hình ảnh so sánh ở các câu trên theo sơ đồ sau:
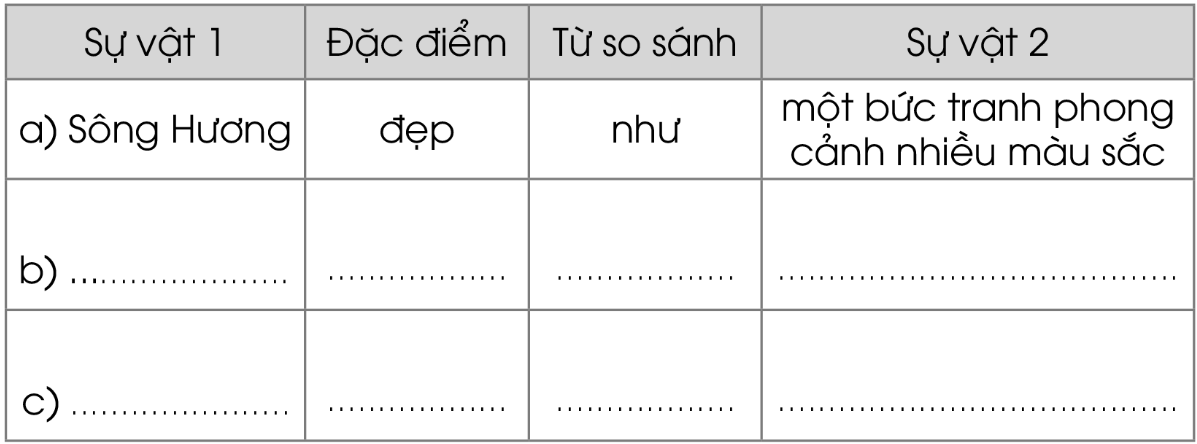
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365