Đoạn chat
{{ u.title == null ? u.user.first_name + ' ' + u.user.last_name : (u.title == '' ? u.user.first_name + ' ' + u.user.last_name : u.title) }}
{{u.count_unread_messages > 99 ? '99+': u.count_unread_messages }}
{{ u.title == null ? u.user.first_name + ' ' + u.user.last_name : (u.title == '' ? u.user.first_name + ' ' + u.user.last_name : u.title) }}
{{ u.title == null ? users[u.user].first_name + ' ' + users[u.user].last_name : (u.title == '' ? users[u.user].first_name + ' ' + users[u.user].last_name : u.title) }}
{{u.count_unread_messages > 99 ? '99+': u.count_unread_messages }}
{{ u.title == null ? users[u.user].first_name + ' ' + users[u.user].last_name : (u.title == '' ? users[u.user].first_name + ' ' + users[u.user].last_name : u.title) }}
{{u.last_message}}
.
{{u.last_message_time}}
Giờ đây, hãy bắt đầu cuộc trò chuyện
Xem thêm các cuộc trò chuyện
Trò chuyện
Tắt thông báo
Bật thông báo
Click Tắt thông báo để không nhận tin nhắn cho đến khi bạn Bật thông báo
Tôi:
{{ name_current_user == '' ? current_user.first_name + ' ' + current_user.last_name : name_current_user }}
Tìm chủ nhân Đại Sảnh Kết Giao.
Trao giải!
{{ u.title == null ? u.user.first_name + ' ' + u.user.last_name : (u.title == '' ? u.user.first_name + ' ' + u.user.last_name : u.title) }}
{{u.count_unread_messages > 99 ? '99+': u.count_unread_messages }}
{{ u.title == null ? u.user.first_name + ' ' + u.user.last_name : (u.title == '' ? u.user.first_name + ' ' + u.user.last_name : u.title) }}
{{ u.title == null ? u.user.first_name + ' ' + u.user.last_name : (u.title == '' ? u.user.first_name + ' ' + u.user.last_name : u.title) }}
{{u.count_unread_messages > 99 ? '99+': u.count_unread_messages }}
{{ u.title == null ? u.user.first_name + ' ' + u.user.last_name : (u.title == '' ? u.user.first_name + ' ' + u.user.last_name : u.title) }}
{{ u.title == null ? u.user.first_name + ' ' + u.user.last_name : (u.title == '' ? u.user.first_name + ' ' + u.user.last_name : u.title) }}
{{u.count_unread_messages > 99 ? '99+': u.count_unread_messages }}
{{ u.title == null ? u.user.first_name + ' ' + u.user.last_name : (u.title == '' ? u.user.first_name + ' ' + u.user.last_name : u.title) }}
{{u.last_message}}
.
{{u.last_message_time}}

Đang trực tuyến

avatar
{{u.first_name}} {{u.last_name}}
Đang hoạt động
Xem thêm
{{c.title}}
{{c.contact.username}}
{{ users[c.contact.id].first_name +' '+ users[c.contact.id].last_name}}
{{c.contact.last_online ? c.contact.last_online : 'Gần đây'}}
Đang hoạt động
Loading…
{{users[m.sender_id].first_name}} {{users[m.sender_id].last_name}} {{users[m.sender_id].first_name}} {{users[m.sender_id].last_name}}
{{check_include_link(m.content)}}
Tin nhắn đã bị xóa
{{m.message_time}}
{{m.content}}

Hiện không thể nhắn tin với người dùng này do đã bị chặn từ trước.

Biểu tượng cảm xúc
😃
☂️
🐱
{{e.code}}

Bài 17. Hàm số liên tục Toán 11 kết nối tri thức

Giải mục 2 trang 120, 121 SGK Toán 11 tập 1 - Kết nối tri thức

Giải mục 3 trang 121,122 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.14 trang 122 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.15 trang 122 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.16 trang 122 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.17 trang 122 SGK Toán 11 tập 1 - Kết nối tri thức Giải mục 1 trang 119, 120 SGK Toán 11 tập 1 - Kết nối tri thức Lý thuyết Hàm số liên tục - SGK Toán 11 Kết nối tri thức
Chat GPT
Trò chuyện
Giải bài tập SGK
Streak
Wheel
Hỏi đáp bài tập
Góc thư giãn
Game365.io
Chữa lỗi ngữ pháp
Learn Anything
Tài liệu giáo viên
Từ vựng
Bài viết
Ngữ pháp
Travelingo
Nối từ
Đánh giá & góp ý

Giải mục 2 trang 120, 121 SGK Toán 11 tập 1 - Kết nối tri thức

Cho hai hàm số (fleft( x right) = left{ {begin{array}{*{20}{c}}{2x;,;0 le x le frac{1}{2}}{1;,frac{1}{2} < x le 1}end{array}} right.) và (gleft( x right) = left{ {begin{array}{*{20}{c}}{x;,0 le x le frac{1}{2}}{1;,frac{1}{2} < x le 1}end{array}} right.)

Cuộn nhanh đến câu

HĐ 2

Cho hai hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{2x\;,\;0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\) và \(g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x\;,0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\)với đồ thị tương ứng như Hình 5.7

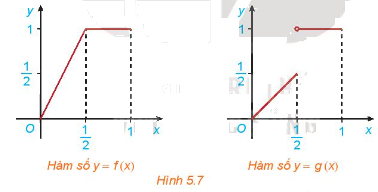
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm \(x = \frac{1}{2}\)và nhận xét về sự khác nhau giữa hai đồ thị.

LT 2

Tìm các khoảng trên đó hàm số \(f\left( x \right) = \frac{{{x^2} + 1}}{{x + 2}}\) liên tục.

Mẹo tìm đáp án nhanh

Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365

Bài tiếp theo: Giải mục 3 trang 121,122 SGK Toán 11 tập 1 - Kết nối tri thức
Bài 5.14 trang 122 SGK Toán 11 tập 1 - Kết nối tri thức
Bài 5.15 trang 122 SGK Toán 11 tập 1 - Kết nối tri thức
Bài 5.16 trang 122 SGK Toán 11 tập 1 - Kết nối tri thức
Bài 5.17 trang 122 SGK Toán 11 tập 1 - Kết nối tri thức
Giải mục 1 trang 119, 120 SGK Toán 11 tập 1 - Kết nối tri thức
Lý thuyết Hàm số liên tục - SGK Toán 11 Kết nối tri thức
Chat GPT
Trò chuyện
Giải bài tập SGK
Streak
Wheel
Hỏi đáp bài tập
Góc thư giãn
Game365.io
Chữa lỗi ngữ pháp
Learn Anything
Tài liệu giáo viên
Từ vựng
Bài viết
Ngữ pháp
Travelingo
Nối từ
Đánh giá & góp ý
Học tập cùng Learn Anything
Chủ đề:

Khái niệm về giai đoạn đầu tiên

Khái niệm về giai đoạn thứ hai và vai trò của nó trong quá trình phát triển, tiến hóa hoặc thay đổi của một hệ thống hoặc quá trình

Khái niệm về sản phẩm acylation và vai trò trong hóa học: cơ chế, tính chất và ứng dụng".

Khái niệm về hợp chất Lewis acid

Clorua nhôm - Hợp chất hóa học quan trọng, ứng dụng rộng rãi trong lĩnh vực hóa học và công nghệ. Cấu trúc phân tử, tính chất và ứng dụng của clorua nhôm.

Axit carboxylic: định nghĩa, cấu trúc, tính chất và ứng dụng trong thực phẩm, dược phẩm và polymer - Tìm hiểu về sự tạo este, thủy phân và oxi hóa của axit carboxylic trong hóa học tổng hợp.

Thuốc nhuận tràng - giới thiệu, cơ chế hoạt động, công dụng, tác dụng phụ và cách sử dụng

Giới thiệu về hợp chất tạo màu

Khái niệm về độ chọn lọc phản ứng

Khái niệm về phương pháp thay thế

Xem thêm...

Cài đặt ứng dụng Baitap365.com, giao diện đẹp hơn trên điện thoại.

×