Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com

Bài 3. Các công thức lượng giác Toán 11 Chân trời sáng tạo
Giải mục 4 trang 22, 23 SGK Toán 11 tập 1 - Chân trời sáng tạo
Bài 1 trang 23 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 2 trang 23 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 3 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 4 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 5 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 7 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 8 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 9 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo Giải mục 3 trang 22 SGK Toán 11 tập 1 - Chân trời sáng tạo Giải mục 2 trang 21, 22 SGK Toán 11 tập 1 - Chân trời sáng tạo Giải mục 1 trang 21 SGK Toán 11 tập 1 - Chân trời sáng tạo Giải hoạt động khởi động trang 20 SGK Toán 11 tập 1 - Chân trời sáng tạo Lý thuyết Các công thức lượng giác - SGK Toán 11 Chân trời sáng tạoGiải mục 4 trang 22, 23 SGK Toán 11 tập 1 - Chân trời sáng tạo
Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác (alpha = frac{{alpha + beta }}{2},beta = frac{{alpha - beta }}{2}) ta được đẳng thức nào?
Hoạt động 4
Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác \(\alpha = \frac{{\alpha + \beta }}{2},\beta = \frac{{\alpha - \beta }}{2}\) ta được đẳng thức nào?
Thực hành 4
Tính \(\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}}\).
Vận dụng
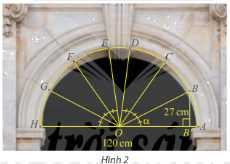
Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính \(\sin \alpha \) và \(\cos \alpha \), từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365