Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 5. Dãy số Toán 11 kết nối tri thức
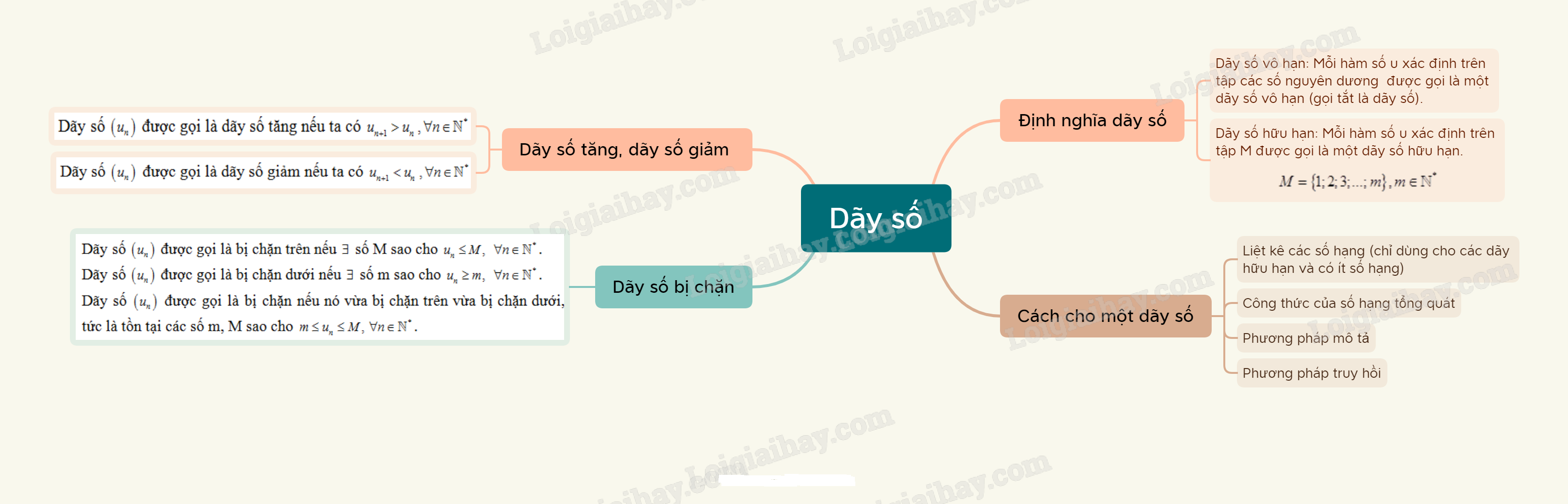
Lý thuyết Dãy số - SGK Toán 11 Kết nối tri thức
Giải mục 1 trang 42, 43 SGK Toán 11 tập 1 - Kết nối tri thức Giải mục 2 trang 43, 44 SGK Toán 11 tập 1 - Kết nối tri thức Giải mục 3 trang 45, 46 SGK Toán 11 tập 1 - Kết nối tri thức Bài 2.1 trang 46 SGK Toán 11 tập 1 - Kết nối tri thức Bài 2.2 trang 46 SGK Toán 11 tập 1 - Kết nối tri thức Bài 2.3 trang 46 SGK Toán 11 tập 1 - Kết nối tri thức Bài 2.4 trang 46 SGK Toán 11 tập 1 - Kết nối tri thức Bài 2.5 trang 46 SGK Toán 11 tập 1 - Kết nối tri thức Bài 2.6 trang 46 SGK Toán 11 tập 1 - Kết nối tri thức Bài 2.7 trang 47 SGK Toán 11 tập 1 - Kết nối tri thứcLý thuyết Dãy số - SGK Toán 11 Kết nối tri thức
1. Định nghĩa dãy số
1. Định nghĩa dãy số
Mỗi hàm số u xác định trên tập các số nguyên dương N∗ được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu là u=u(n).
Ta thường viết un thay cho u(n) và kí hiệu dãy số u=u(n)bởi u(n), do đó dãy số (un)được viết dưới dạng khai triển u1,u2,u3,...,un,...
Số u1 là số hạng đầu; unlà số hạng thứ n và gọi là số hạng tổng quát của dãy số.
*Chú ý: Nếu ∀n∈N∗,un=cthì (un)được gọi là dãy số không đổi.
Mỗi hàm số u xác định trên tập M={1;2;3;...;m},m∈N∗ được gọi là một dãy số hữu hạn.
Dạng khai triển của dãy số hữu hạn là u1,u2,u3,...,um.
Số u1 gọi là số hạng đầu, umlà số hạng cuối.
2. Cách cho một dãy số
Một dãy số có thể cho bằng:
3. Dãy số tăng, dãy số giảm và dãy số bị chặn
Dãy số (un) được gọi là dãy số giảm nếu ta có un+1<un,∀n∈N∗.
Dãy số (un) được gọi là bị chặn dưới nếu ∃ số m sao cho un≥m, ∀n∈N∗.
Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho m≤un≤M,∀n∈N∗.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365