Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 1. Dãy số Toán 11 Cùng khám phá
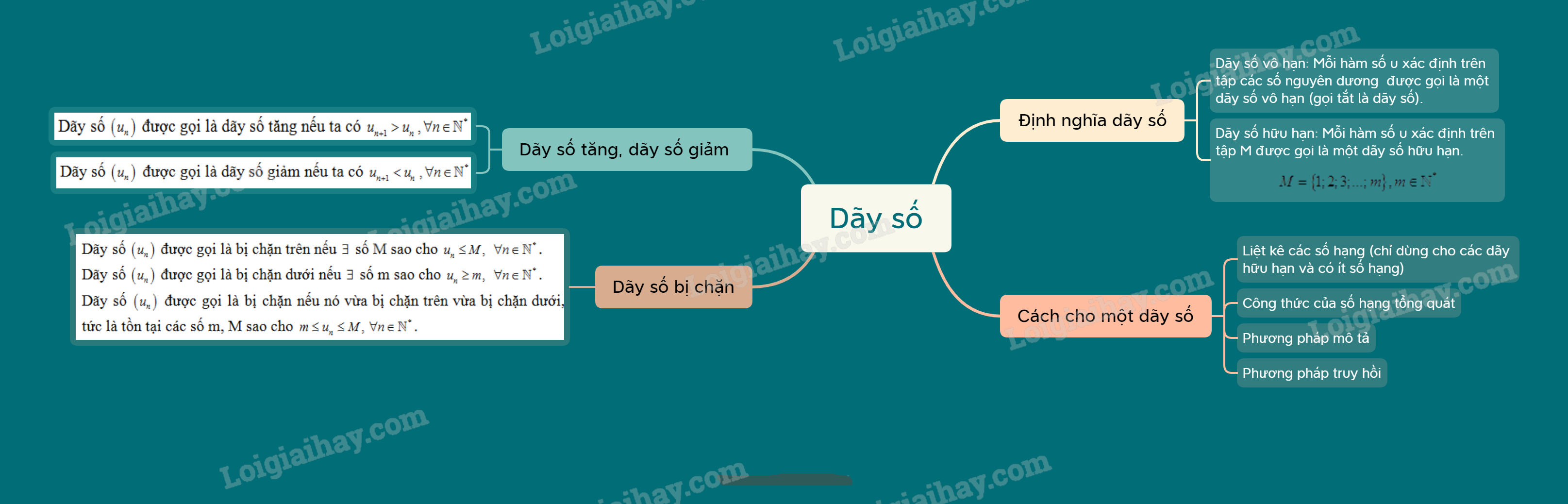
Lý thuyết Dãy số - SGK Toán 11 Cùng khám phá
Giải mục 1 trang 50, 51 SGK Toán 11 tập 1 - Cùng khám phá Giải mục 2 trang 45, 46, 47 SGK Toán 11 tập 1 - Cùng khám phá Giải mục 3 trang 47, 48, 49 SGK Toán 11 tập 1 - Cùng khám phá Bài 2.1 trang 49 SGK Toán 11 tập 1 - Cùng khám phá Bài 2.2 trang 49 SGK Toán 11 tập 1 - Cùng khám phá Bài 2.3 trang 49 SGK Toán 11 tập 1 - Cùng khám phá Bài 2.4 trang 49 SGK Toán 11 tập 1 - Cùng khám phá Bài 2.5 trang 49 SGK Toán 11 tập 1 - Cùng khám pháLý thuyết Dãy số - SGK Toán 11 Cùng khám phá
1. Dãy số
1. Dãy số
- Một hàm sốu=u(n)u=u(n) xác định trên tập các số nguyên dương N∗ được gọi là một dãy số vô hạn (gọi tắt là dãy số).
Kí hiệu là u(n)=un hay dãy số (un).
- Một hàm số u=u(n) xác định trên tập M={1;2;3;...;m},m∈N∗ được gọi là một dãy số hữu hạn.
*Nhận xét:
- Dãy số (un) được viết dưới dạng khai triển u1,u2,u3,...,un,... Số u1 là số hạng đầu; un là số hạng thứ n và gọi là số hạng tổng quát của dãy số; n được gọi là chỉ số.
- Dạng khai triển của dãy số hữu hạn là u1,u2,u3,...,um. Trong đó, số u1 gọi là số hạng đầu, um là số hạng cuối.
II. Cách cho một dãy số
Một dãy số có thể cho bằng:
- Cho số hạng thứ nhất u1 (hoặc một vài số hạng đầu tiên)
- Cho một công thức tính un theoun−1 (hoặc theo vài số hạng đứng ngay trước nó).
III. Dãy số tăng, dãy số giảm và dãy số bị chặn
1. Dãy số tăng, dãy số giảm
2. Dãy số bị chặn
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365