Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 2. Đường đi Euler và đường đi Hamilton Chuyên đề học tập Toán 11 Chân trời sáng tạo
Giải mục 1 trang 50, 51, 52, 53, 54 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Giải mục 2 trang 54, 55, 56, 57, 58 Chuyên đề học tập Toán 11 - Chân trời sáng tạo Giải bài 1 trang 58 Chuyên đề học tập Toán 11 Chân trời sáng tạo Giải bài 2 trang 58 Chuyên đề học tập Toán 11 Chân trời sáng tạo Giải bài 3 trang 58 Chuyên đề học tập Toán 11 Chân trời sáng tạo Giải bài 4 trang 58 Chuyên đề học tập Toán 11 Chân trời sáng tạo Giải bài 5 trang 59 Chuyên đề học tập Toán 11 Chân trời sáng tạo Giải bài 6 trang 59 Chuyên đề học tập Toán 11 Chân trời sáng tạo Giải khởi động trang 49 Chuyên đề học tập Toán 11 - Chân trời sáng tạoGiải mục 1 trang 50, 51, 52, 53, 54 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Nếu coi mỗi vùng đất của thành phố Königsberg là một đỉnh, mỗi cây cầu là một cạnh nối hai đỉnh thì ta được một đồ thị G như Hình 1.
Khám phá 1
a) Nếu coi mỗi vùng đất của thành phố Königsberg là một đỉnh, mỗi cây cầu là một cạnh nối hai đỉnh thì ta được một đồ thị G như Hình 1.
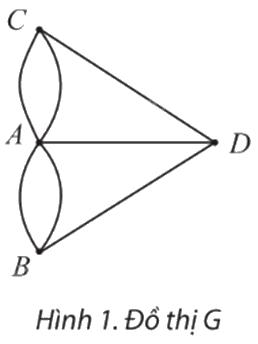
Câu hỏi của người dân thành phố trở thành: có hay không cách vẽ bằng một nét bút liền (không nhấc bút) đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng một lần, sao cho điểm kết thúc trùng với điểm xuất phát?
Hãy thử vẽ và đưa ra dự đoán của mình.
b) Nếu không có cây cầu nối giữa A và D nhưng có thêm một cây cầu nối B và C thì ta có đồ thị H như Hình 2. Có thể vẽ một nét liền đi qua tất cả các cạnh của đồ thị này, mỗi cạnh đúng một lần không?
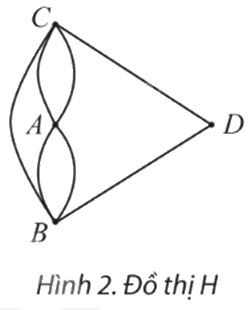
Khám phá 2
a) Chỉ ra một chu trình Euler của đồ thị G ở Hình 5. Đồ thị này có đỉnh nào bậc lẻ không?
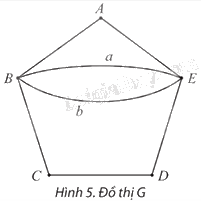
b) Chỉ ra rằng các đồ thị S và T sau đây không có chu trình Euler. Các đồ thị này có đỉnh bậc lẻ không?

Khám phá 3
Hãy chỉ ra một đường đi Euler trên mỗi đồ thị sau. Mỗi đồ thị có bao nhiêu đỉnh bậc lẻ?
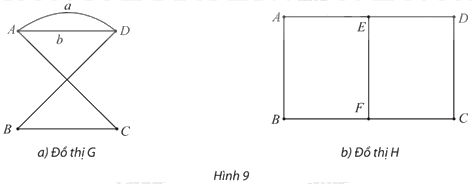
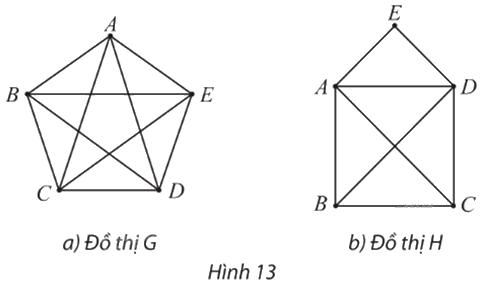
Thực hành 1
Mỗi đồ thị sau đây có chu trình Euler không? Nếu có, hãy chỉ ra một chu trình như vậy.
Thực hành 2
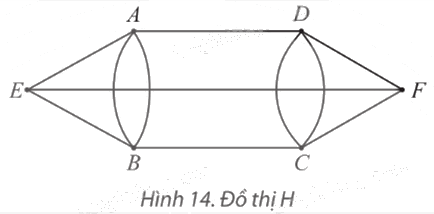
Đồ thị sau có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.
Vận dụng 1
Hãy giải đáp câu hỏi của người dân Königsberg ở Hoạt động khởi động (còn gọi là bài toán Bảy cây cầu).
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365