Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 19. Lôgarit Toán 11 Kết nối tri thức
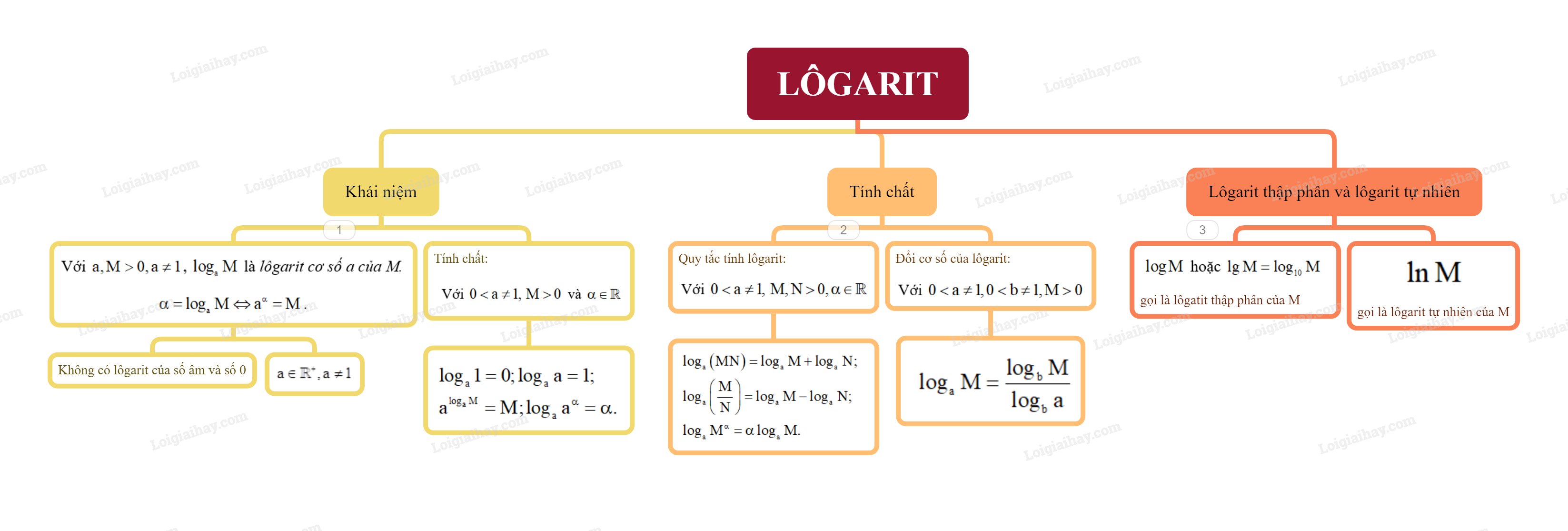
Lý thuyết Lôgarit - Toán 11 Kết nối tri thức
Giải mục 1 trang 10, 11 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 2 trang 11, 12, 13 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 3 trang 14 SGK Toán 11 tập 2 - Kết nối tri thức Bài 6.9 trang 14 SGK Toán 11 tập 2 - Kết nối tri thức Bài 6.10 trang 14 SGK Toán 11 tập 2 - Kết nối tri thức Bài 6.11 trang 15 SGK Toán 11 tập 2 - Kết nối tri thức Bài 6.12 trang 15 SGK Toán 11 tập 2 - Kết nối tri thức Bài 6.13 trang 15 SGK Toán 11 tập 2 - Kết nối tri thức Bài 6.14 trang 15 SGK Toán 11 tập 2 - Kết nối tri thứcLý thuyết Lôgarit - Toán 11 Kết nối tri thức
1. Khái niệm Lôgarit
1. Khái niệm Lôgarit
Cho a là một số thực dương khác 1 và M là một số thực dương. Số thực αα để aα=Maα=M được gọi là lôgarit cơ số a của M và kí hiệu là logaMlogaM.
α=logaM⇔aα=Mα=logaM⇔aα=M.
Chú ý: Không có lôgarit của số âm và số 0. Cơ số của lôgarit phải dương và khác 1. Từ định nghĩa lôgarit, ta có các tính chất sau:
Với 0<a≠1,M>00<a≠1,M>0 và αα là số thực tùy ý, ta có:
loga1=0;logaa=1;alogaM=M;logaaα=α.
2. Tính chất của lôgarit
a) Quy tắc tính lôgarit
Giả sử a là số thực dương khác 1, M và N là các số thực dương, α là số thực tùy ý. Khi đó:
loga(MN)=logaM+logaN;loga(MN)=logaM−logaN;logaMα=αlogaM.
b) Đổi cơ số của lôgarit
Với các cơ số lôgarit a và b bất kì (0<a≠1,0<b≠1) và M là số thực dương tùy ý, ta luôn có:
logaM=logbMlogba.
3. Lôgarit thập phân và lôgarit tự nhiên
a) Lôgarit thập phân
Lôgarit cơ số 10 của một số dương M gọi là lôgatit thập phân của M, kí hiệu là logM hoặc lgM (đọc là lốc của M).
b) Số e và lôgarit tự nhiên
Lôgarit cơ số e của một số dương M gọi là lôgarit tự nhiên của M, kí hiệu là lnM (đọc là lôgarit Nêpe của M).
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365