1. Phép chiếu vuông góc

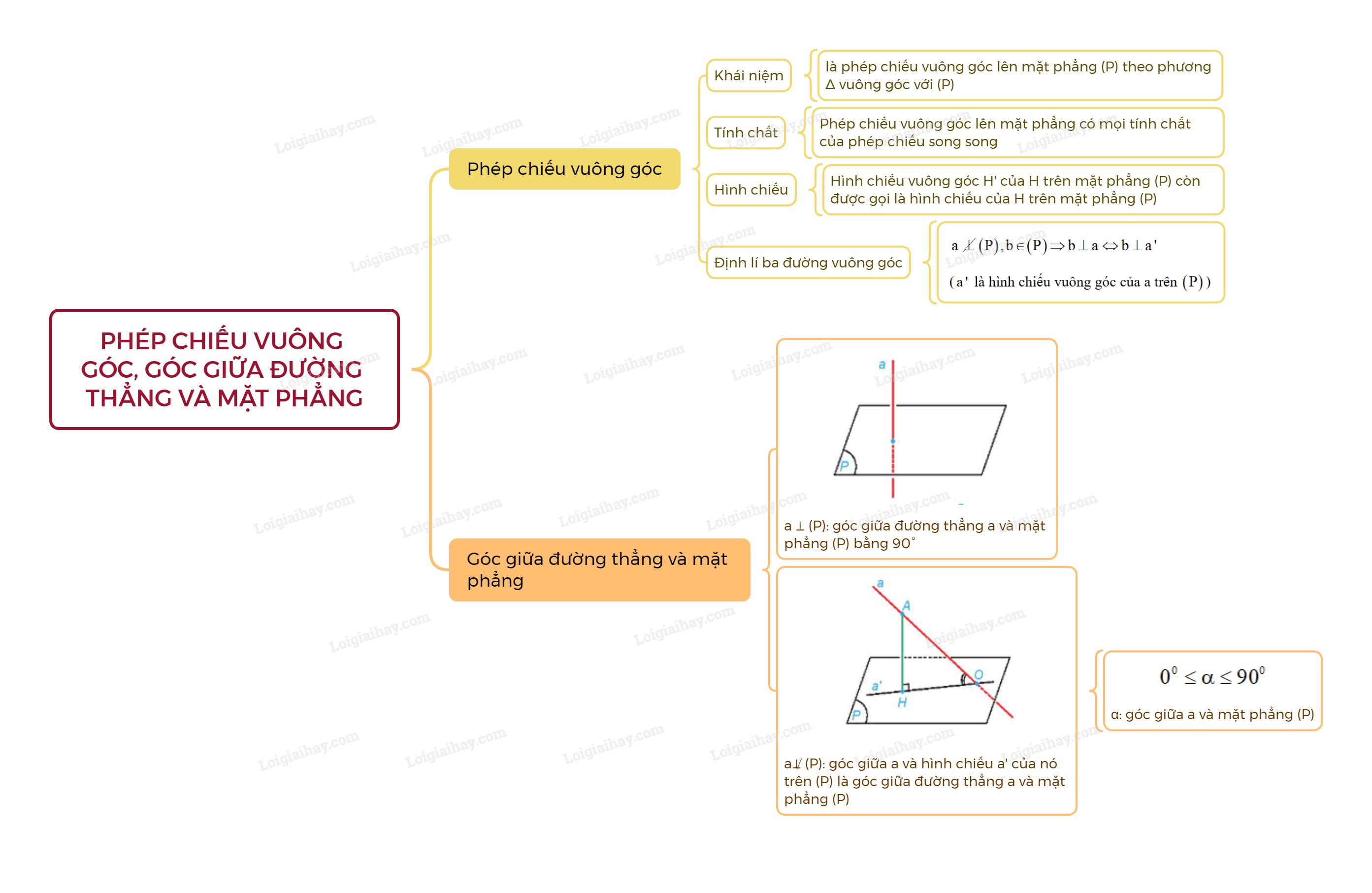
Phép chiếu vuông góc lên mặt phẳng (P) theo phương $\Delta$ vuông góc với (P) được gọi là phép chiều vuông góc lên mặt phẳng (P).

Chú ý:

- Vì phép chiếu vuông góc lên một mặt phẳng là một trường hợp đặc biệt của phép chiếu song song nên nó có mọi tính chất của phép chiếu song song.

- Phép chiếu vuông góc lên mặt phẳng (P) còn được gọi đơn giản là phép chiếu lên mặt phẳng (P). Hình chiếu vuông góc H’ của hình H trên mặt phẳng (P) còn được gọi là hình chiếu của H trên mặt phẳng (P).

Định lí ba đường vuông góc:

Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Khi đó, một đường thẳng b nằm trong mặt phẳng (P) vuông góc với đường thẳng a khi và chỉ khi b vuông góc với hình chiếu vuông góc a’ của a trên (P).

2. Góc giữa đường thẳng và mặt phẳng

Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mặt phẳng (P) bằng ${90^0}$.

Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a’ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P).

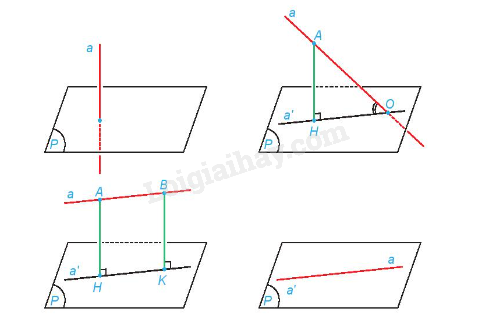
Chú ý: Nếu $\alpha$ là góc giữa đường thẳng a và mặt phẳng (P) thì ${0^0} \le \alpha  \le {90^0}$.

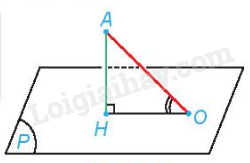
Nhận xét: Nếu điểm A có hình chiếu H trên mặt phẳng (P). Lấy điểm O thuộc mặt phẳng (P), O không trung H. Khi đó góc giữa đường thẳng AO và mặt phẳng (P) bằng góc AOH.