Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 2. Phép tính lôgarit Toán 11 Chân trời sáng tạo
Lý thuyết Phép tính lôgarit - Toán 11 Chân trời sáng tạo
Giải mục 1 trang 14, 15 SGK Toán 11 tập 2 - Chân trời sáng tạo Giải mục 2 trang 16 SGK Toán 11 tập 2 - Chân trời sáng tạo Giải mục 3 trang 16, 17 SGK Toán 11 tập 2 - Chân trời sáng tạo Giải mục 4 trang 18, 19 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 1 trang 19 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 2 trang 19 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 3 trang 19 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 4 trang 19 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 5 trang 19 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 6 trang 19 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 7 trang 19 SGK Toán 11 tập 2 - Chân trời sáng tạoLý thuyết Phép tính lôgarit - Toán 11 Chân trời sáng tạo
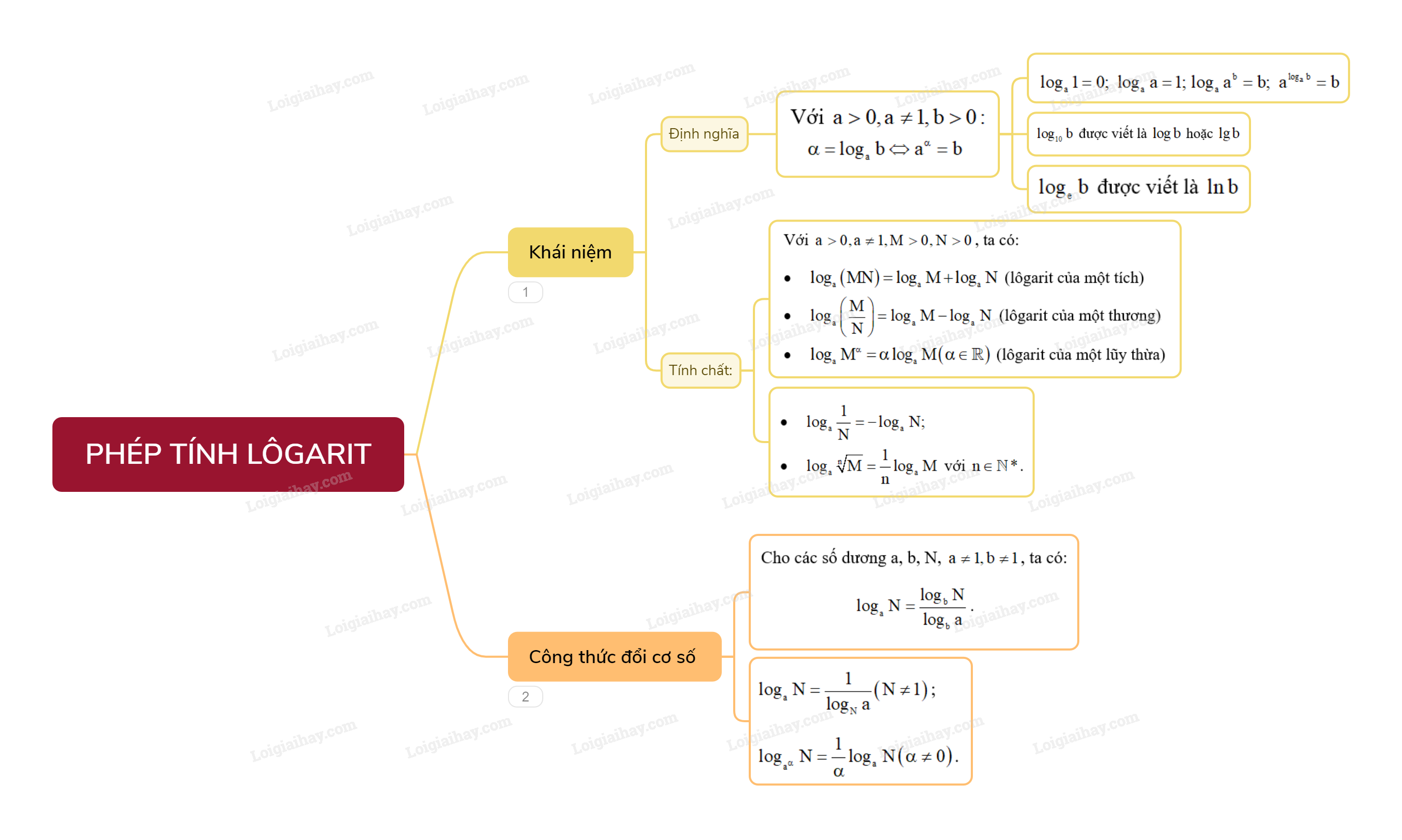
1. Khái niệm lôgarit Cho hai số thực dương a, b với a≠1a≠1. Số thực αα thỏa mãn đẳng thức aα=baα=b được gọi là lôgarit cơ số a của b và kí hiệu là logablogab.
1. Khái niệm lôgarit
Cho hai số thực dương a, b với a≠1a≠1. Số thực αα thỏa mãn đẳng thức aα=baα=b được gọi là lôgarit cơ số a của b và kí hiệu là logablogab.
α=logab⇔aα=bα=logab⇔aα=b.
Chú ý:
Từ định nghĩa, ta có:
2. Tính chất
Với a>0,a≠1,M>0,N>0a>0,a≠1,M>0,N>0, ta có:
Chú ý: Đặc biệt, ta có:
3. Công thức đổi cơ số
Cho các số dương a, b, N, a≠1,b≠1, ta có:
logaN=logbNlogba.
Đặc biệt, ta có:
logaN=1logNa(N≠1); logaαN=1αlogaN(α≠0).
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365