Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 11 Cánh diều - Đề số 4
Phần trắc nghiệm (7 điểm) Câu 1: Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
Đáp án : B
Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0, ta có a−n=1an.
4−6=146
Đáp án B.
Chọn đáp án đúng.
Cho số thực a và số nguyên dương n (n≥2). Số b được gọi là căn bậc n của số a nếu:
Đáp án : B
Cho số thực a và số nguyên dương n (n≥2). Số b được gọi là căn bậc n của số a nếu bn=a.
Cho số thực a và số nguyên dương n (n≥2). Số b được gọi là căn bậc n của số a nếu bn=a.
Đáp án B.
Chọn đáp án đúng:
Đáp án : A
n√an=a khi n lẻ (với các biểu thức đều có nghĩa).
3√(1−√5)3=1−√5.
Đáp án A.
Rút gọn biểu thức (93+√3−9√3−1).3−2√3 được kết quả là:
Đáp án : A
Với a là số thực dương, α,β là những số thực bất kì thì: (aα)β=aαβ,aα.aβ=aα+β.
Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0, ta có a−n=1an.
(93+√3−9√3−1).3−2√3=(32(3+√3)−32(√3−1)).3−2√3=36+2√3−2√3−32√3−2−2√3=36−3−2=36−132=65609
Đáp án A.
Cho a, b là các số thực dương. Rút gọn biểu thức (4√a3b2)83√√a12b6
Đáp án : D
n√an=|a| nếu n là số chẵn.
m√n√a=mn√a (các biểu thức đều có nghĩa)
(4√a3b2)83√√a12b6=((4√a3b2)4)26√(a2b)6=(a3b2)2a2b=a6b4a2b=a4b3
Đáp án D.
Chọn đáp án đúng.
Đáp án : A
Với số thực dương a, b và a≠1 thì:
+ logaab=b
+ logeb được viết là ln b
lne2=2
Đáp án A.
Chọn đáp án đúng.
Cho a, b là các số thực dương. Giá trị của lnab+lnba bằng:
Đáp án : D
Với số thực dương a, b, c và a≠1 thì:
+ logeb được viết là ln b.
+ loga1=0, loga(bc)=logab+logac.
lnab+lnba=ln(ab.ba)=ln1=0
Đáp án D.
Chọn đáp án đúng.
Cho a>0,a≠1,b>0. Với mọi số nguyên dương n≥2 ta có:
Đáp án : B
Cho a>0,a≠1,b>0. Với mọi số nguyên dương n≥2 ta có logan√b=1nlogab.
Cho a>0,a≠1,b>0. Với mọi số nguyên dương n≥2 ta có logan√b=1nlogab.
Đáp án B.
Cho logab=4. Giá trị của loga(a3b2) bằng:
Đáp án : D
+ Với a, b là số thực dương và a≠1 thì logaaα=α,logabα=αlogab
+ Với 0<a≠1,b,c>0 thì loga(bc)=logab+logac.
loga(a3b2)=logaa3+logab2=3+2logab=3+2.4=11
Đáp án D.
Cho hai số thực dương a, b thỏa mãn a3b2=1000. Giá trị của biểu thức P=3loga+2logb là:
Đáp án : C
+ Với a, b là số thực dương và a≠1 thì logaaα=α,logabα=αlogab.
+ Với 0<a≠1,b,c>0 thì loga(bc)=logab+logac.
P=3loga+2logb=loga3+logb2=log(a3b2)=log1000=log103=3
Đáp án C.
Trong các hàm số dưới đây, hàm số nào nghịch biến trên (0;+∞)?
Đáp án : B
Với 0<a<1 thì hàm số y=logax(a>0,a≠1) nghịch biến trên (0;+∞).
Vì 0<1π<1 nên hàm số y=log1πx nghịch biến trên (0;+∞).
Đáp án B.
Hàm số nào dưới đây là hàm số đồng biến trên R?
Đáp án : A
Với a>1 thì hàm số y=ax(a>0,a≠1) đồng biến trên R.
Vì 3>1 nên hàm số y=3x đồng biến trên R.
Đáp án A.
Đồ thị hàm số y=62x luôn đi qua điểm nào dưới đây?
Đáp án : A
Đồ thị hàm số y=ax(a>0,a≠1) luôn đi qua điểm (0; 1).
Đồ thị hàm số y=62x luôn đi qua điểm (0; 1).
Đáp án A.
Chọn đáp án đúng.
Hàm số y=logx có cơ số là:
Đáp án : B
Hàm số y=logax(a>0,a≠1) được gọi là hàm số lôgarit cơ số a.
Hàm số y=logx có cơ số là 10.
Đáp án B.
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số y=logax,y=logbx,y=logcx thể hiện ở hình vẽ dưới đây.
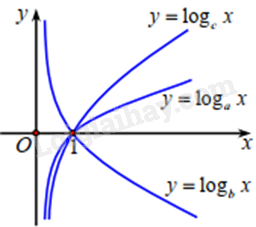
Khẳng định nào dưới đây là đúng?
Đáp án : A
Nếu 0<a<1 thì hàm số y=logax(a>0,a≠1) nghịch biến trên (0;+∞).
Nếu a>1 thì hàm số y=logax(a>0,a≠1) đồng biến trên (0;+∞).
Ta thấy hàm số y=logbx nghịch biến trên (0;+∞) nên b<1.
Hàm số y=logax,y=logcx đồng biến trên (0;+∞) nên a>1,c>1.
Xét tại một điểm x>1 thì: logcx>logax⇒logcx>1logxa⇒logcx.logxa>1⇒a>c
Do đó, b<c<a.
Đáp án A.
Tập xác định của hàm số y=1√3−x+ln(x−1) là:
Đáp án : C
Hàm số y=lnu(x) xác định khi u(x)>0.
Hàm số y=1√u(x) xác định khi u(x)>0.
Hàm số y=1√3−x+ln(x−1) xác định khi {3−x>0x−1>0⇔{x<3x>1
Vậy tập xác định của hàm số là: D=(1;3).
Đáp án C.
Thống kê chiều cao của 40 học sinh lớp 11A (đơn vị: cm), ta có bảng số liệu sau:

Giá trị đại diện của nhóm [160;165) là:
Đáp án : B
Mỗi nhóm số liệu gồm một số giá trị của mẫu số liệu được ghép nhóm theo một tiêu chí xác định có dạng [a;b). Giá trị đại diện của nhóm [a;b) là xi=a+b2.
Giá trị đại diện của nhóm [160;165) là: 160+1652=162,5(cm)
Đáp án B.
Nếu hai biến cố A và B độc lập và P(A)=0,7,P(AB)=0,28 thì:
Đáp án : B
Nếu hai biến cố A và B độc lập thì P(A∩B)=P(A).P(B).
Vì hai biến cố A và B độc lập nên P(A∩B)=P(A).P(B)⇒P(B)=P(A∩B)P(A)=0,280,7=0,4
Đáp án B.
Bảng tần số ghép nhóm cho ở bảng dưới:
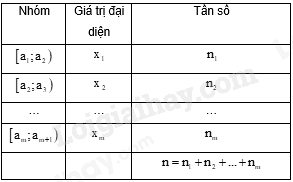
Giá trị trung bình ¯x của nhóm mẫu số liệu là:
Đáp án : D
Bảng tần số ghép nhóm cho ở bảng dưới:
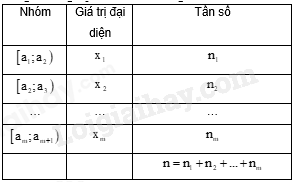
+ Trung điểm xi của nửa khoảng (tính bằng trung bình cộng hai đầu mút) ứng với nhóm i là giá trị đại diện của nhóm đó.
+ Số trung bình cộng của mẫu số liệu ghép nhóm, kí hiệu ¯x, được tính theo công thức: ¯x=n1x1+n2x2+...+nmxmn
Số trung bình cộng của mẫu số liệu ghép nhóm, kí hiệu ¯x, được tính theo công thức: ¯x=n1x1+n2x2+...+nmxmn
Đáp án D.
Chọn đáp án đúng.
Trong hộp kín có 6 quả bóng màu xanh và 8 quả bóng màu đỏ, các quả bóng có kích thước và khối lượng giống nhau. Lấy ngẫu nhiên đồng thời 2 quả bóng. Xét các biến cố:
A: “Hai quả bóng lấy ra có màu xanh”;
B: “Hai quả bóng lấy ra có màu đỏ”.
Biến cố hợp của hai biến cố A và B là:
Đáp án : A
Biến cố A∪B có thể phát biểu dưới đạng mệnh đề nêu sự kiện là: “A xảy ra hoặc B xảy ra” hay “Có ít nhất một trong các biến cố A, B xảy ra”.
Biến cố hợp của hai biến cố A và B là: Hai quả bóng lấy ra cùng có màu đỏ hoặc màu xanh
Đáp án A.
Một đội văn nghệ có 4 học sinh nam và 5 học sinh nữ. Giao viên phụ trách muốn chọn ra một đội tốp ca gồm 3 học sinh sao cho có cả nam và nữ cùng tham gia. Giáo viên có bao nhiêu cách chọn đội tốp ca như vậy?
Đáp án : A
+ Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu Ω. Đặt C=A∪B, ta có C là một biến cố và được gọi là biến cố hợp của hai biến cố A và B, kí hiệu là A∪B.
+ Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu Ω. Đặt C=A∩B, ta có C là một biến cố và được gọi là biến cố giao của hai biến cố A và B, kí hiệu là C=A∩B hay AB.
Xét các biến cố:
H: “Trong 3 học sinh chọn ra có cả nam và nữ”.
A: “Trong 3 học sinh chọn ra có 2 học sinh nam và 1 học sinh nữ”.
B: “Trong 3 học sinh chọn ra có 1 học sinh nam và 2 học sinh nữ”.
Khi đó, H=A∪B và A∩B=∅
Do A và B là hai biến cố xung khắc nên n(H)=n(A)+n(B).
Số các kết quả thuận lợi cho biến cố A là: n(A)=C24.C15=4!2!.2!.5!1!.4!=6.5=30
Số các kết quả thuận lợi cho biến cố B là: n(B)=C14.C25=4!1!.3!.5!2!.3!=4.10=40
Số các kết quả thuận lợi cho biến cố H là: n(H)=n(A)+n(B)=30+40=70
Vậy có 70 cách chọn một đội tốp ca gồm 3 học sinh sao cho có cả nam và nữ cùng tham gia.
Đáp án A.
Cho A và B là hai biến cố độc lập với nhau. Biết rằng P(A)=0,8 và P(AB)=0,4. Xác suất của biến cố ¯A¯B là:
Đáp án : C
Nếu hai biến cố A và B độc lập thì P(A∩B)=P(A).P(B).
Do A và B là hai biến cố độc lập P(B)=P(AB)P(A)=0,40,8=0,5
Vì ¯A là biến cố đối của biến cố A nên P(¯A)=1−P(A)=1−0,8=0,2.
Vì ¯B là biến cố đối của biến cố B nên P(¯B)=1−P(B)=1−0,5=0,5.
Xác suất của biến cố ¯A¯B là: P(¯A¯B)=P(¯A)P(¯B)=0,2.0,5=0,1
Đáp án C.
Bảng tần số ghép nhóm số liệu dưới đây thống kê kết quả kiểm môn toán của lớp 11E như sau:
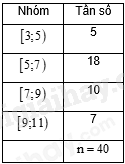
Mốt của mẫu số liệu ghép nhóm trên là (làm tròn kết quả đến hàng phần mười):
Đáp án : C
Bảng tần số ghép nhóm cho ở bảng dưới:

Giả sử nhóm i là nhóm có tần số lớn nhất. Ta gọi u, g, ni lần lượt là đầu mút trái, độ dài, tần số của nhóm i; ni−1,ni+1 lần lượt là tần số của nhóm i−1;i+1. Mốt của mẫu số liệu ghép nhóm, kí hiệu Mo được tính theo công thức sau: Mo=u+(ni−ni−12ni−ni−1−ni+1).g.
Ta thấy: Nhóm 2 ứng với nửa khoảng [5;7) là nhóm có tần số lớn nhất với u=5;g=2,n2=18. Nhóm 1 có tần số n1=5 và nhóm 3 có tần số n3=10.
Mốt của mẫu số liệu là: Mo=5+18−52.18−5−10.2≈6,2
Đáp án C.
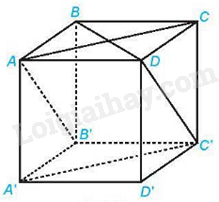
Cho hình hộp ABCD.A’B’C’D’ có các mặt là các hình vuông. Góc giữa hai đường thẳng AA’ và CD bằng:
Đáp án : A
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu (a,b) hoặc ^(a;b).
Vì AB//CD nên (AA′,CD)=(AA′,AB)=900
Đáp án A.
Cho tứ diện ABCD. Lấy điểm I bất kì thuộc cạnh AC. Qua I kẻ đường thẳng song song với AB cắt BC tại M. Qua I kẻ đường thẳng song song với CD cắt AD tại N. Khi đó, góc giữa hai đường thẳng AB và CD là:
Đáp án : C
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu (a,b) hoặc ^(a;b).
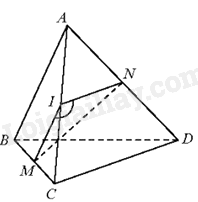
Vì MI//AB, IN//CD nên (AB,CD)=(IM,IN).
Đáp án C.
Cho hình chóp S. ABCD có ABCD là hình vuông cạnh bằng a và các cạnh bên đều bằng a. Gọi M, N lần lượt là trung điểm của AD, SD. Góc giữa hai đường thẳng MN và SC bằng:
Đáp án : A
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu (a,b) hoặc ^(a;b).
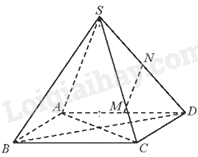
Vì M, N lần lượt là trung điểm của AD, SD nên MN là đường trung bình của tam giác SAD. Do đó, MN//AS. Suy ra, (MN,SC)=(SA,SC)=^SAC.
Vì tam giác ABC vuông tại B nên AC2=AB2+BC2=2a2
Vì AC2=SA2+AC2 nên tam giác SAC vuông tại S (định lí Pythagore đảo)
Do đó, ^ASC=900. Vậy (MN,SC)=900.
Đáp án A.
Cho hình chóp S. ABCD với đáy ABCD có tất cả các cạnh bằng nhau. Gọi I, J lần lượt thuộc các cạnh SC, BC sao cho tam giác IJC là tam giác đều. Khi đó, góc giữa hai đường thẳng IJ và AD bằng:
Đáp án : A
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu (a,b) hoặc ^(a;b).
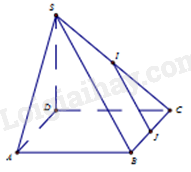
Tứ giác ABCD có: AB=BC=CD=DA nên tứ giác ABCD là hình thoi. Do đó, AD//BC.
Suy ra: (IJ,AD)=(IJ,BC)=^CJI
Tam giác IJC là tam giác đều nên ^IJC=600. Do đó, góc giữa hai đường thẳng IJ và AD bằng 600.
Đáp án A.
Cho hình chóp S.ABC có SA⊥(ABC). Khẳng định nào sau đây là đúng?
Đáp án : A
Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
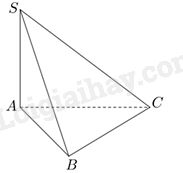
Vì SA⊥(ABC) và AB,BC,CA⊂(ABC) nên SA⊥BC, SA⊥AC, SA⊥AB.
Đáp án D.
Cho hình hộp ABCD.A’B’C’D’ có AA′⊥(ABCD). Khẳng định nào dưới đây đúng?
Đáp án : B
Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
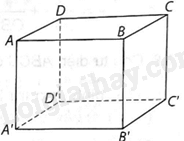
Vì AA′⊥(ABCD) và AA’//BB’ nên BB′⊥(ABCD)
Đáp án B.
Trong không gian, cho điểm A và mặt phẳng (P). Mệnh nào dưới đây đúng?
Đáp án : B
Có đúng một đường thẳng đi qua A và vuông góc với (P).
Có đúng một đường thẳng đi qua A và vuông góc với (P).
Đáp án B.
Phát biểu nào sau đây là đúng?
Đáp án : D
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau trong mặt phẳng (P) thì d vuông góc với (P).
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau trong mặt phẳng (P) thì d vuông góc với (P).
Đáp án D.
Cho tứ diện ABCD có ABC và BCD là các tam giác cân tại A và D. Gọi I là trung điểm của BC. Kẻ AH⊥DI(H∈DI). Hình chiếu vuông góc của A trên mặt phẳng (BCD) là:
Đáp án : B
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì d⊥(P).
+ Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P).
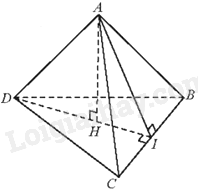
Vì tam giác ABC cân tại A nên AI là đường trung tuyến đồng thời là đường cao. Do đó, AI⊥BC.
Vì tam giác DBC cân tại D nên DI là đường trung tuyến đồng thời là đường cao. Do đó, DI⊥BC.
Ta có: AI⊥BC, DI⊥BC, DI và AI cắt nhau tại I và nằm trong mặt phẳng (AID) nên BC⊥(AID). Mà AH⊂(ADI)⇒AH⊥CB
Lại có: AH⊥DI, DI và BC cắt nhau tại I và nằm trong mặt phẳng (BCD). Do đó, AH⊥(BCD). Do đó, hình chiếu vuông góc của A trên mặt phẳng (BCD) là điểm H.
Đáp án B.
Cho hình chóp S. ABC có SA⊥(ABC), M là trung điểm của BC. Tam giác ABC cân tại A. Mệnh đề nào sau đây sai?
Đáp án : A
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì d⊥(P).
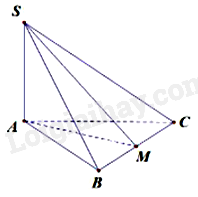
Vì SA⊥(ABC),BC⊂(ABC)⇒SA⊥BC
Tam giác ABC cân tại A nên AM là đường trung tuyến đồng thời là đường cao.
Do đó, BC⊥AM
Vì SA⊥BC, BC⊥AM, SA và AM cắt nhau tại A và nằm trong mặt phẳng (SAM) nên BC⊥(SAM), mà SM⊂(SAM)⇒BC⊥SM
Tam giác SBC có BC⊥SM nên BC không thể vuông góc với SB. Do đó, câu A sai.
Đáp án A.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi và SA=SC,SB=SD. Gọi O là giao điểm của AC và BD. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là:
Đáp án : C
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì d⊥(P).
+ Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P).
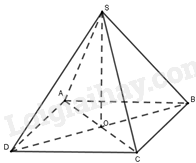
Vì ABCD là hình thoi, O là giao điểm của AC và BD nên O là trung điểm của AC, O là trung điểm của BD.
Vì SA=SC nên tam giác SAC cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác. Suy ra, SO⊥AC.
Vì SB=SD nên tam giác SBD cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác. Suy ra, SO⊥BD.
Vì SO⊥AC, SO⊥BD và BD và AC cắt nhau tại O và nằm trong mặt phẳng (ABCD) nên SO⊥(ABCD). Do đó, hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm O.
Đáp án C.
Cho tứ diện ABCD có DA⊥(ABC), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Góc giữa hai đường thẳng GK và AB bằng:
Đáp án : C
Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
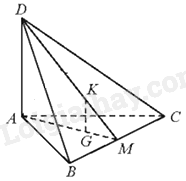
Vì K là trọng tâm của tam giác DBC, DM là đường trung tuyến của tam giác DBC nên MKMD=13
Vì G là trọng tâm của tam giác ABC, AM là đường trung tuyến của tam giác ABC nên MGMA=13
Tam giác DMA có: MKMD=MGMA(=13) nên GK//AD
Mà AD⊥(ABC) suy ra GK⊥(ABC). Mà AB⊂(ABC)⇒GK⊥AB
Do đó, góc giữa hai đường thẳng GK và AB bằng 900.
Đáp án C.
Cho hàm số: y=log[(m−2)x2+2(m+1)x+2m].
a) Với m=3, hãy tìm tập xác định của hàm số trên.
b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định với mọi giá trị thực của x.
Hàm số y=logu(x) xác định khi u(x)>0.
a) Với m=3 ta có: y=log(x2+8x+6).
Hàm số y=log(x2+8x+6) xác định khi x2+8x+6>0⇔[x>−4+√10x<−4−√10
Vậy với m=3 thì tập xác định của hàm số là: D=(−∞;−4−√10)∪(−4+√10;+∞).
b) Hàm số y=log[(m−2)x2+2(m+1)x+2m] xác định với mọi giá trị thực của x khi và chỉ khi f(x)=(m−2)x2+2(m+1)x+2m>0 với mọi x∈R
Trường hợp 1: Với m=2 ta có: f(x)=6x+4>0⇔x>−23.
Do đó, f(x) không xác định với mọi giá trị thực của x. Do đó, m=2 không thỏa mãn.
Trường hợp 2: Với m≠2.
Hàm số f(x)=(m−2)x2+2(m+1)x+2m>0 với mọi x∈R
⇔{m−2>0Δ′=(m+1)2−(m−2)2m<0⇔{m>2−m2+6m+1<0⇔{m>2[m<3−√10m>3+√10⇔m>3+√10
Vậy với m∈(3+√10;+∞) thì hàm số y=log[(m−2)x2+2(m+1)x+2m] có tập xác định với mọi giá trị thực của x.
Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và B, SA⊥(ABCD), AD=2a,AB=BC=a. Chứng minh rằng:
a) Tam giác SBC là tam giác vuông.
b) CD⊥SC.
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì d⊥(P).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
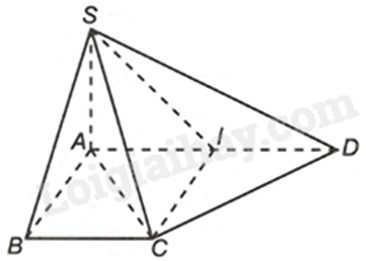
a) Vì SA⊥(ABCD),BC⊂(ABCD)⇒SA⊥BC.
Vì ABCD là hình thang vuông tại A và B nên AB⊥BC.
Ta có: SA⊥BC, AB⊥BC, SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB) nên BC⊥(SAB). Lại có, SB⊂(SBC)⇒BC⊥SB. Suy ra, tam giác SBC vuông tại B.
b) Gọi I là trung điểm của AD. Do đó, AI=ID=12AD=a
Tứ giác ABCI có: AI//BC (do tứ giác ABCD là hình thang vuông tại A, B), AI=BC(=a) nên tứ giác ABCI là hình bình hành. Lại có: BC=AB nên tứ giác ABCI là hình thoi. Mà ^BAI=900 nên ABCI là hình vuông. Do đó, ^AIC=900⇒^CID=900
Tam giác CID có: ^CID=900,CI=ID(=a) nên tam giác CID vuông cân tại I.
Suy ra: ^DCI=450.
Lại có: CA là phân giác góc ICB (do ABCI là hình vuông) nên ^ACI=12^ICB=12.900=450
Suy ra: ^ACD=^ACI+^ICD=900 hay AC⊥CD
Vì SA⊥(ABCD),DC⊂(ABCD)⇒SA⊥DC
Ta có: AC⊥CD, SA⊥DC, SA và AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên DC⊥(SAC). Mà SC⊂(SAC)⇒CD⊥SC
Ông A gửi tiền tiết kiệm vào ngân hàng với hình thức cứ mỗi đầu tháng đóng 5 triệu đồng với lãi suất 0,3%/tháng. Tính số tiền mà ông A thu được từ ngân hàng sau 5 năm.
an=a.a...a(a∈R,n∈N∗) (có n thừa số a)
Đặt a=5 triệu đồng, r=0,33%.
Gọi Pn là số tiền ông A thu được sau n tháng (n≥1)
Sau tháng thứ nhất, ông A tiết kiệm được: P1=a(1+r) (triệu đồng)
Sau tháng thứ hai, ông A tiết kiệm được:
P2=(P1+a)(1+r)=[a(1+r)+a](1+r)=a(1+r)2+a(1+r) (triệu đồng)
Sau tháng thứ ba, ông A tiết kiệm được: P3=(P2+a)(1+r)=a(1+r)3+a(1+r)2+a(1+r) (triệu đồng)
…
Sau tháng thứ n, ông A tiết kiệm được: Pn=(Pn−1+a)(1+r)=a(1+r)n+a(1+r)n−1+...+a(1+r) (triệu đồng)
Xét cấp số nhân có số hạng đầu u1=a(1+r) và công bội q=1+r thì Pn=u1+u2+...+un=u1.1−qn1−q
Vậy số tiền ông A nhận được từ ngân hàng sau 5 năm là:
P60=u1.1−q601−q=5.1,003.1−1,00360−0,003≈329 (triệu đồng)
Vậy sau 5 năm ông A thu được từ ngân hàng khoảng 329 triệu đồng.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365