Câu 1: Cho biểu thức $P = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}} + \frac{{\sqrt x {\rm{ \;}} + 1}}{{\sqrt x {\rm{ \;}} - 2}} - \frac{{2 + 5\sqrt x }}{{x - 4}}$ với $x \ge 0,x \ne 4$.

1. Rút gọn biểu thức P

2. Tìm tất cả các giá trị của $x$ để $P > 1$.

Câu 2: 

1. Trong mặt phẳng tọa độ Oxy, cho đường thẳng $(d)$ có phương trình $y = ax + b$. Tìm a, b để đường thẳng $(d)$ có hệ số góc bằng 3 và đi qua điểm $M( - 1;2).$

2. Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x + y = 6}\\{x - y = {\rm{ \;}} - 2}\end{array}} \right.$

Câu 3: 

1. Giải phương trình ${x^2} - 3x + 2 = 0$.

2. Cho phương trình ${x^2} - 2mx - {m^2} - 2 = 0$ ( $m$ là tham số). Tìm các giá trị của $m$ để phương trình có hai nghiệm ${x_1},{x_2}$ (với ${x_1} < {x_2}$ ) thỏa mãn hệ thức ${x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4$.  

Câu 4: Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ điểm M kẻ hai tiếp tuyến MA, MB đến (O) (với A, B là các tiếp điểm). Gọi C là điểm đối xứng với B qua O, đường thẳng MC cắt đường tròn (O) tại D (D khác C).

1. Chứng minh MAOB là tứ giác nội tiếp.

2. Gọi N là giao điểm của hai đường thẳng AD và MO. Chứng minh rằng MN² = ND.NA.

3. Gọi H là giao điểm của MO và AB. Chứng minh ${\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1$.

Câu 5: Cho các số thực không âm x, y, z thỏa mãn $4{x^2} + {y^2} + 4{z^2} \le 6y$.

Tìm giá trị nhỏ nhất của biểu thức $M = \frac{8}{{{{(x + 3)}^2}}} + \frac{{16}}{{{{(y + 4)}^2}}} + \frac{1}{{{{(z + 1)}^2}}} + 2023$.

----- HẾT -----

Câu 1 (VD):

Phương pháp:

1. Quy đồng và rút gọn.

2. Giải phương trình P > 1.

Cách giải:

1. Rút gọn biểu thức P

Ta có $P = \frac{{\sqrt x }}{{\sqrt x  + 2}} + \frac{{\sqrt x  + 1}}{{\sqrt x  - 2}} - \frac{{2 + 5\sqrt x }}{{x - 4}}$

             $\begin{array}{l} = \frac{{\sqrt x \left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} + \frac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} - \frac{{2 + 5\sqrt x }}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\ = \frac{{x - 2\sqrt x  + x + 3\sqrt x  + 2 - 2 - 5\sqrt x }}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\ = \frac{{2x - 4\sqrt x }}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\ = \frac{{2\sqrt x \left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\ = \frac{{2\sqrt x }}{{\sqrt x  + 2}}\end{array}$

Vậy $P = \frac{{2\sqrt x }}{{\sqrt x  + 2}}$ với $x \ge 0,x \ne 4$

2. Tìm tất cả các giá trị của $x$ để $P > 1$.

Để $P > 1$

$\frac{{2\sqrt x }}{{\sqrt x  + 2}} > 1 \Leftrightarrow 2\sqrt x  > \sqrt x  + 2$  (do $\sqrt x  + 2$ > 0)

$\begin{array}{l} \Leftrightarrow \sqrt x  > 2\\ \Leftrightarrow x > 4\end{array}$

Đối chiếu với điều kiện $x \ge 0,x \ne 4$, để P > 1 thì $x > 4$

Câu 2 (VD):

Phương pháp:

1. $y = ax + b$ có hệ số góc là a.

2. Sử dụng phương pháp thế hoặc trừ vế.

Cách giải:

1. Trong mặt phẳng tọa độ Oxy, cho đường thẳng $(d)$ có phương trình $y = ax + b$. Tìm a, b để đường thẳng $(d)$ có hệ số góc bằng 3 và đi qua điểm $M( - 1;2).$

Vì (d) có hệ số góc bằng 3 nên suy ra: $a = 3.$

Khi đó phương trình đường thẳng (d) có dạng $y = 3x + b$

Vì (d) đi qua điểm $M( - 1;2)$ nên thay tọa độ điểm M vào phương trình đường thẳng (d) ta được:

$2 = 3.\left( { - 1} \right) + b \Leftrightarrow 2 =  - 3 + b \Leftrightarrow b = 5$

Vậy $a = 3;\,\,b = 5.$

2. Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x + y = 6}\\{x - y =  - 2}\end{array}} \right.$

Ta có: $\left\{ {\begin{array}{*{20}{l}}{3x + y = 6}\\{x - y =  - 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x = 4}\\{y = x + 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 3}\end{array}} \right.} \right.$

Vậy hệ phương trình có nghiệm duy nhất là: $\left( {x;y} \right) = \left( {1;3} \right)$.

Câu 3 (NB):

Phương pháp:

1. Bước 1: Tính giá trính của $\Delta$ với $\Delta \; = {{\rm{b}}^2} - 4{\rm{ac}}$

Bước 2: Xét tập nghiệm của phương trình bằng việc sánh giá $\Delta$ với 0

$\Delta \; < 0 \Rightarrow$ phương trình bậc 2 vô nghiệm

$\Delta \; = 0 \Rightarrow$ phương trình bậc 2 có nghiệm kép ${x_1} = {x_2} = \; - \frac{b}{{2a}}$

$\Delta \; > 0 \Rightarrow$ phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau: ${x_{1,2}} = \frac{{ - b \pm \sqrt \Delta  {\rm{ \;}}}}{{2a}}$.

2. Sử dụng Vi et.

Cách giải:

1. Giải phương trình ${x^2} - 3x + 2 = 0$.

Xét  phương trình ${x^2} - 3x + 2 = 0$ có $a + b + c = 0$ nên ta có phương trình có hai nghiệm phân biệt $\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \frac{c}{a} = 2\end{array} \right.$

Vậy phương trình có hai nghiệm phân biệt $\left[ \begin{array}{l}{x_1} = 1\\{x_2} = 2\end{array} \right.$.

2. Cho phương trình ${x^2} - 2mx - {m^2} - 2 = 0$ ( $m$ là tham số). Tìm các giá trị của $m$ để phương trình có hai nghiệm ${x_1},{x_2}$ (với ${x_1} < {x_2}$ ) thỏa mãn hệ thức ${x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4$. 

Xét phương trình ${x^2} - 2mx - {m^2} - 2 = 0$ có $\Delta ' = {\left( { - m} \right)^2} - 1.\left( { - {m^2} - 2} \right) = {m^2} + {m^2} + 2 = 2{m^2} + 2 > 0$ với mọi m.

Áp dụng định lí Vi – ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} =  - {m^2} - 2\end{array} \right.$ .        (2)

Nhận thấy ${x_1}{x_2} =  - {m^2} - 2 < 0$ với mọi m nên phương trình có hai nghiệm trái dấu ${x_1} < 0 < {x_2}$.

$\begin{array}{l}{x_2} - 2\left| {{x_1}} \right| - 3{x_1}{x_2} = 3{m^2} + 3m + 4\\ \Leftrightarrow {x_2} + 2{x_1} - 3{x_1}{x_2} = 3{m^2} + 3m + 4\\ \Leftrightarrow 2{x_1} + {x_2} - 3\left( { - {m^2} - 2} \right) = 3{m^2} + 3m + 4\\ \Leftrightarrow 2{x_1} + {x_2} + 3{m^2} + 6 = 3{m^2} + 3m + 4\\ \Leftrightarrow 2{x_1} + {x_2} = 3m - 2\end{array}$

Ta có hệ phương trình $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\2{x_1} + {x_2} = 3m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = m - 2\\{x_2} = 2m - m + 2 = m + 2\end{array} \right.$

Thay vào ${x_1}{x_2} =  - {m^2} - 2$ ta được phương trình

$\begin{array}{l}\left( {m - 2} \right)\left( {m + 2} \right) =  - {m^2} - 2\\ \Leftrightarrow {m^2} - 4 =  - {m^2} - 2\\ \Leftrightarrow 2{m^2} = 2\end{array}$

$\begin{array}{l} \Leftrightarrow {m^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m =  - 1\end{array} \right.\end{array}$

Vậy $\left[ \begin{array}{l}m = 1\\m =  - 1\end{array} \right.$ thỏa mãn yêu cầu bài toán.

Câu 4 (VD):

Cách giải:

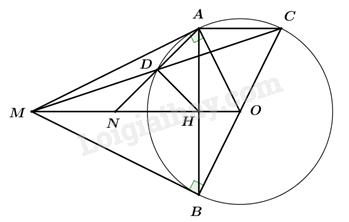
1. Chứng minh MAOB là tứ giác nội tiếp.

Vì MA, MB là tiếp tuyến của (O) (gt) $\Rightarrow \angle MAO = \angle MBO = {90^0}$.

$\Rightarrow \angle MAO + \angle MBO = {90^0} + {90^0} = {180^0}$.

Mà A, B là hai đỉnh đối diện của tứ giác MAOB.

Vậy MAOB là tứ giác nội tiếp (dhnb).

2. Gọi N là giao điểm của hai đường thẳng AD và MO. Chứng minh rằng MN² = ND.NA.

Ta có: $\angle MDN = \angle ADC$ (đối đỉnh), $\angle ADC = \angle ABC$ (hai góc nội tiếp cùng chắn cung AC)

$\Rightarrow \angle MDN = \angle ABC$.

Mà $\angle ABC = \angle ABO = \angle AMO = \angle AMN$ (hai góc nội tiếp cùng chắn cung AO).

$\Rightarrow \angle MDN = \angle AMN$.

Xét $\Delta MND$ và $\Delta ANM$ có:

$\begin{array}{l}\angle ANM\,\,chung\\\angle MDN = \angle AMN\,\,\left( {cmt} \right)\end{array}$

$\Rightarrow \Delta MND\backsim \Delta ANM\,\,\left( g.g \right)$

$\Rightarrow \frac{{MN}}{{NA}} = \frac{{ND}}{{MN}}$ (cặp cạnh tương ứng tỉ lệ) $\Rightarrow M{N^2} = ND.NA\,\,\left( {dpcm} \right)$.

3. Gọi H là giao điểm của MO và AB. Chứng minh ${\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1$.

Xét $\Delta MAD$ và $\Delta MCA$ có:

$\angle AMC$ chung

$\angle MAD = \angle MCA$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AD).

$\Rightarrow \Delta MAD\backsim \Delta MCA\,\,\left( g.g \right)$

$\Rightarrow \frac{{MA}}{{MC}} = \frac{{MD}}{{MA}}$ (cặp cạnh tương ứng tỉ lệ)

$\Rightarrow M{A^2} = MC.MD$                   (1)

Ta có: $OA = OB\,\,\left( { = R} \right) \Rightarrow O$ thuộc trung trực của AB.

$MA = MB$ (tính chất hai tiếp tuyến cắt nhau) $\Rightarrow M$ thuộc trung trực của AB.

$\Rightarrow OM$ là trung trực của AB $\Rightarrow OM \bot AB$ tại H.

Xét tam giác OAM vuông tại A có đường cao AH, áp dụng hệ thức lượng trong tam giác vuông ta có:

$M{A^2} = MH.MO$                  (2)

Từ (1), (2) $\Rightarrow MC.MD = MH.MO \Rightarrow \frac{{MC}}{{MH}} = \frac{{MO}}{{MD}}$.

Xét $\Delta MOC$ và $\Delta MDH$ có:

$\angle OMC$ chung

$\frac{{MC}}{{MH}} = \frac{{MO}}{{MD}}\,\,\left( {cmt} \right)$

$\Rightarrow \Delta MOC\backsim \Delta MDH\,\,\left( g.g \right)$

$\Rightarrow \angle MHD = \angle MCO$ (hai góc tương ứng)

Mà $\angle MCO = \angle DCB = \angle DAB$ (hai góc nội tiếp cùng chắn cung DB)

$\Rightarrow \angle MHD = \angle DAB$.

Mà $\angle MHD + \angle DHA = \angle AHM = {90^0}$.

$\Rightarrow \angle DAB + \angle DHA = {90^0}$ $\Rightarrow \Delta ADH$ vuông tại D (tam giác có tổng hai góc bằng ${90^0}$).

$\Rightarrow HD \bot AN$ tại D.

Áp dụng định lí Pytago trong tam giác vuông ADH có: $H{A^2} = A{D^2} + H{D^2}$.

Biến đổi ${\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1$ ta có:

$\begin{array}{l}{\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1 \Leftrightarrow \frac{{A{D^2} + H{D^2}}}{{H{D^2}}} = 1 + \frac{{AC}}{{HN}}\\ \Leftrightarrow \frac{{A{D^2}}}{{H{D^2}}} + 1 = 1 + \frac{{AC}}{{HN}} \Leftrightarrow \frac{{A{D^2}}}{{H{D^2}}} = \frac{{AC}}{{HN}}\end{array}$

Xét tam giác AHN vuông tại H, có đường cao HD ta có: $H{D^2} = AD.DN$ (hệ thức lượng trong tam giác vuông)

$\Rightarrow \frac{{A{D^2}}}{{H{D^2}}} = \frac{{AC}}{{HN}} \Leftrightarrow \frac{{A{D^2}}}{{AD.DN}} = \frac{{AC}}{{HN}} \Rightarrow \frac{{AD}}{{DN}} = \frac{{AC}}{{HN}} \Leftrightarrow \frac{{AD}}{{AC}} = \frac{{DN}}{{HN}}$.

Xét $\Delta ADC$ và $\Delta NDM$ có:

$\angle ADC = \angle MDN$ (đối đỉnh)

$\angle BAC = {90^0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow AC \bot AB$. Lại có $OM \bot AB\,\,\left( {cmt} \right) \Rightarrow OM//AC$ (từ vuông góc đến song song) $\Rightarrow \angle DAC = \angle DNM$ (so le trong)

$\Rightarrow \Delta ADC\backsim \Delta NDM\,\,\left( g.g \right)$

$\Rightarrow \frac{{AD}}{{AC}} = \frac{{DN}}{{NM}}$ (cặp cạnh tương ứng tỉ lệ).

Suy ra ${\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1 \Leftrightarrow \frac{{DN}}{{NM}} = \frac{{DN}}{{HN}} \Leftrightarrow NM = HN$

Do đó ta cần chứng minh $NM = HN$.

Theo ý 2. ta có: $M{N^2} = ND.NA$.

Áp dụng hệ thức lượng trong tam giác vuông AHN đường cao HD ta có: $N{H^2} = ND.NA$.

Vậy $M{N^2} = N{H^2} \Leftrightarrow MN = NH$. Do đó ta có điều phải chứng minh ${\left( {\frac{{HA}}{{HD}}} \right)^2} - \frac{{AC}}{{HN}} = 1$.

Câu 5 (VDC):

Cách giải:

Áp dụng bất đẳng thức Cosi ta có:

$\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} \ge 2\sqrt {\frac{1}{{{a^2}}}.\frac{1}{{{b^2}}}}  = \frac{2}{{ab}}$

$ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}$

$\Rightarrow \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} \ge \frac{8}{{{{\left( {a + b} \right)}^2}}}$

Khi đó ta có:

$M = \frac{8}{{{{(x + 3)}^2}}} + \frac{{16}}{{{{(y + 4)}^2}}} + \frac{1}{{{{(z + 1)}^2}}} + 2023$

$\,\,\,\,\,\,\, = \frac{8}{{{{(x + 3)}^2}}} + \frac{1}{{{{\left( {\frac{y}{4} + 1} \right)}^2}}} + \frac{1}{{{{(z + 1)}^2}}} + 2023$

$\,\,\,\,\,\,\, \ge \frac{8}{{{{(x + 3)}^2}}} + \frac{8}{{{{\left( {\frac{y}{4} + 1 + z + 1} \right)}^2}}} + 2023$

$\,\,\,\,\,\,\, \ge \frac{{64}}{{{{\left( {x + 3 + \frac{y}{4} + 1 + z + 1} \right)}^2}}} + 2023$

$\,\,\,\,\,\,\, \ge \frac{{64}}{{{{\left( {x + \frac{y}{4} + z + 5} \right)}^2}}} + 2023$

Mặt khác, áp dụng bất đẳng thức Cô-si ta có:

$4{x^2} + 4 \ge 2\sqrt {4{x^2}.4}  = 8x$

${y^2} + 16 \ge 2\sqrt {{y^2}.16}  = 8y$

$4{z^2} + 4 \ge 2\sqrt {4{z^2}.4}  = 8z$

Suy ra: $8x + 8y + 8z \le 4{x^2} + 4 + {y^2} + 16 + 4{z^2} + 4 = 4{x^2} + {y^2} + 4{z^2} + 24$

Mà: $4{x^2} + {y^2} + 4{z^2} \le 6y$

$\begin{array}{l} \Rightarrow 8x + 8y + 8z \le 6y + 24\\ \Leftrightarrow 8x + 2y + 8z \le 24\\ \Leftrightarrow x + \frac{y}{4} + z \le 3\end{array}$

$\begin{array}{l}M \ge \frac{{64}}{{{{\left( {x + \frac{y}{4} + z + 5} \right)}^2}}} + 2023\\\,\,\,\,\,\, = \frac{{64}}{{{{\left( {3 + 5} \right)}^2}}} + 2023 = 2024\end{array}$

Dấu “=” xảy ra khi và chỉ khi $x = z = 1;y = 4$

Vậy giá trị nhỏ nhất của M là 2024 khi $x = z = 1;y = 4.$