Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 8. Khai căn bậc hai với phép nhân và phép chia - Toán 9 Kết nối tri thức
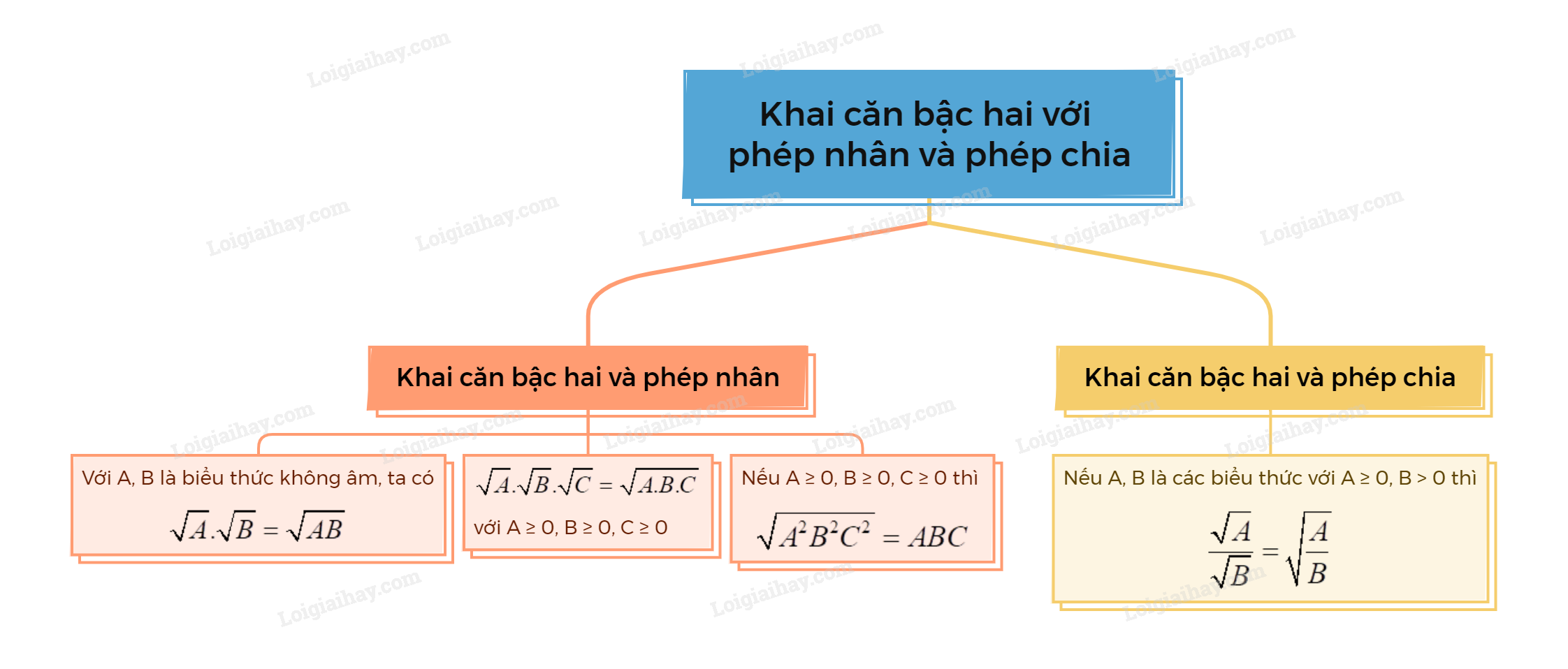
Lý thuyết Khai căn bậc hai với phép nhân và phép chia Toán 9 Kết nối tri thức
Giải mục 1 trang 49, 50 SGK Toán 9 tập 1 - Kết nối tri thức Giải mục 2 trang 50, 51 SGK Toán 9 tập 1 - Kết nối tri thức Giải bài tập 3.7 trang 51 SGK Toán 9 tập 1 - Kết nối tri thức Giải bài tập 3.8 trang 51 SGK Toán 9 tập 1 - Kết nối tri thức Giải bài tập 3.9 trang 51 SGK Toán 9 tập 1 - Kết nối tri thức Giải bài tập 3.10 trang 51 SGK Toán 9 tập 1 - Kết nối tri thức Giải bài tập 3.11 trang 51 SGK Toán 9 tập 1 - Kết nối tri thứcLý thuyết Khai căn bậc hai với phép nhân và phép chia Toán 9 Kết nối tri thức
1. Khai căn bậc hai và phép nhân Liên hệ giữa phép khai căn bậc hai và phép nhân
1. Khai căn bậc hai và phép nhân
Liên hệ giữa phép khai căn bậc hai và phép nhân
|
Với A, B là biểu thức không âm, ta có √A.√B=√AB. |
Ví dụ:
√27.√3=√27.3=√81=9
√5(√125+√5)=√5.√125+√5.√5=√5.125+√5.5=25+5=30
Chú ý:
- Kết quả trên có thể mở rộng cho nhiều biểu thức không âm, chẳng hạn:
√A.√B.√C=√A.B.C (với A≥0,B≥0,C≥0).
Ví dụ: √3.√5.√15=√3.5.15=√225=15
- Nếu A≥0,B≥0,C≥0 thì √A2B2C2=ABC.
Ví dụ: Với a≥0,b<0 thì √25a2b2=√52.a2.(−b)2=√52.√a2.√(−b)2=5.a.(−b)=−5ab
2. Khai căn bậc hai và phép chia
Liên hệ giữa phép khai căn bậc hai và phép chia
|
Nếu A, B là các biểu thức với A≥0,B>0 thì √A√B=√AB. |
Ví dụ: √8√2=√82=√4=2;
Với a>0 thì √52a3√13a=√52a313a=√4a2=√(2a)2=2a.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365