Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 2. Bất phương trình bậc nhất một ẩn - Toán 9 Chân trời sáng tạo
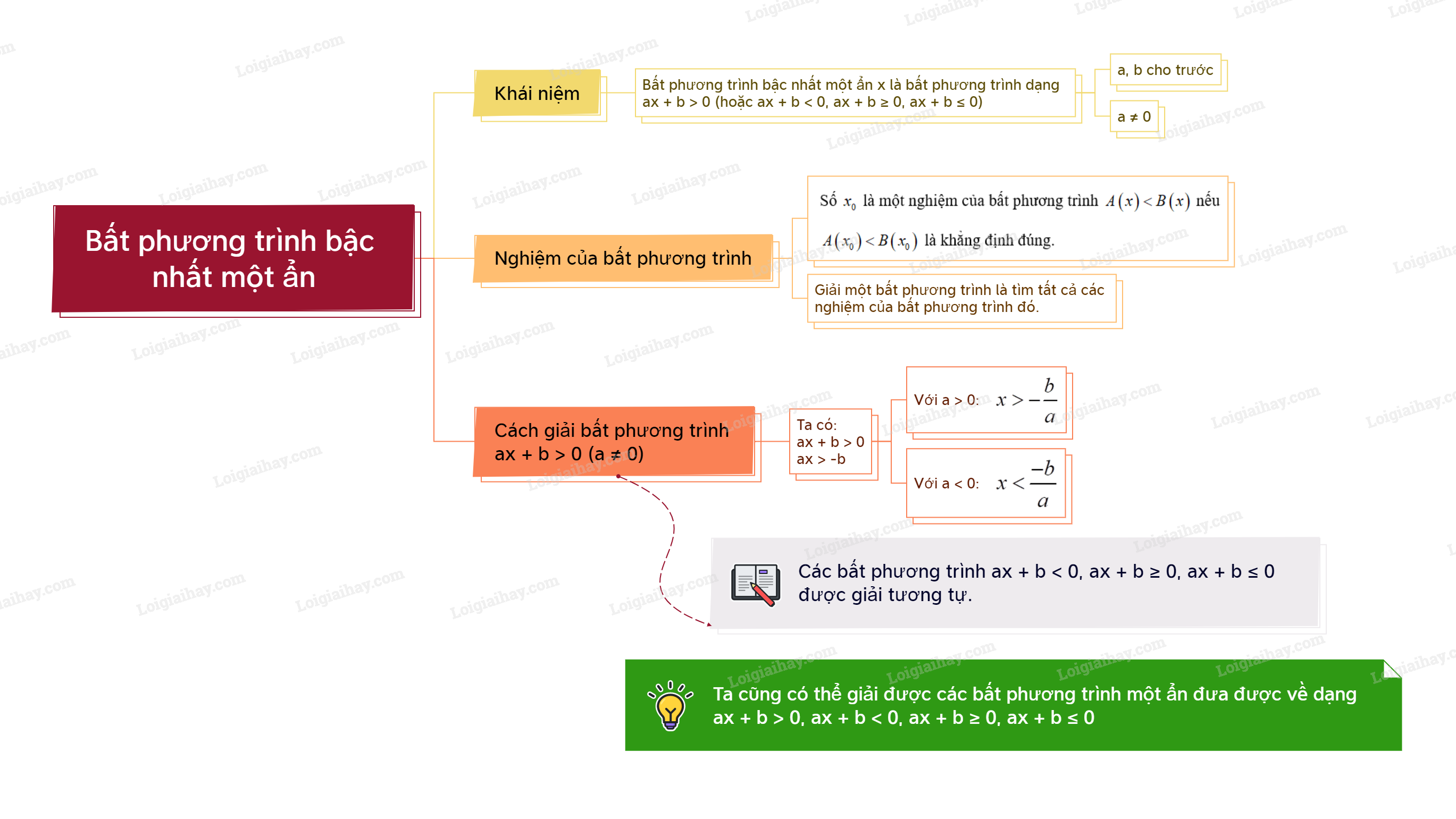
Lý thuyết Bất phương trình bậc nhất một ẩn Toán 9 Chân trời sáng tạo
Giải mục 1 trang 30, 31 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải mục 2 trang 32, 33 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải bài tập 1 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải bài tập 2 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải bài tập 3 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải bài tập 4 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải bài tập 5 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải bài tập 6 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạoLý thuyết Bất phương trình bậc nhất một ẩn Toán 9 Chân trời sáng tạo
1. Bất phương trình bậc nhất một ẩn, nghiệm của bất phương trình bậc nhất một ẩn Khái niệm bất phương trình bậc nhất một ẩn
1. Bất phương trình bậc nhất một ẩn, nghiệm của bất phương trình bậc nhất một ẩn
Khái niệm bất phương trình bậc nhất một ẩn
|
Bất phương trình dạng ax+b<0ax+b<0 (hoặc ax+b>0ax+b>0; ax+b≤0ax+b≤0; ax+b≥0ax+b≥0) trong đó a, b là hai số đã cho, a≠0a≠0 được gọi là bất phương trình bậc nhất một ẩn (ẩn là x). |
Ví dụ: 3x+16≤03x+16≤0; −3x>0−3x>0 là các bất phương trình bậc nhất một ẩn x.
x2−4≥0x2−4≥0 không phải là một bất phương trình bậc nhất một ẩn x vì x2−4x2−4 là một đa thức bậc hai.
3x−2y<23x−2y<2 không phải là một bất phương trình bậc nhất một ẩn vì đa thức 3x−2y3x−2y là đa thức với hai biến x và y.
Nghiệm của bất phương trình
|
Với bất phương trình bậc nhất có ẩn là x, số x0x0 được gọi là một nghiệm của bất phương trình nếu ta thay x=x0x=x0 thì nhận được một khẳng định đúng. Giải bất phương trình là tìm tất cả các nghiệm của nó. |
Ví dụ:
x=−2x=−2 là nghiệm của bất phương trình 2x−10<02x−10<0 vì 2.(−2)−10=−4−10=−14<02.(−2)−10=−4−10=−14<0.
x=6x=6 không là nghiệm của bất phương trình 2x−10<02x−10<0 vì 2.6−10=12−10=2>02.6−10=12−10=2>0.
2. Giải bất phương trình bậc nhất một ẩn
|
Xét bất phương trình ax+b>0(a≠0)ax+b>0(a≠0). - Cộng hai vế của bất phương trình với –b, ta được bất phương trình: ax>−bax>−b. - Nhân hai vế của bất phương trình nhận được với 1a1a: + Nếu a>0a>0 thì nhận được nghiệm của bất phương trình đã cho là: x>−bax>−ba. + Nếu a<0a<0 thì nhận được nghiệm của bất phương trình đã cho là: x<−bax<−ba. |
Chú ý: Với các bất phương trình ax+b<0ax+b<0, ax+b≤0ax+b≤0, ax+b≥0ax+b≥0, ta thực hiện các bước giải tương tự.
Ví dụ: Giải bất phương trình −2x−4>0−2x−4>0
Lời giải: Ta có:
−2x−4>0−2x>0+4−2x>4x<4.(−12)x<−2
Vậy nghiệm của bất phương trình là x<−2.
Chú ý: Bằng cách sử dụng các tính chất của bất đẳng thức, ta có thể giải một số bất phương trình đưa được về bất phương trình bậc nhất một ẩn ax+b<0, ax+b>0, ax+b≤0, ax+b≥0.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365