Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 18. Phương trình quy về phương trình bậc hai Toán 10 Kết nối tri thức
Lý thuyết Phương trình quy về phương trình bậc hai - SGK Toán 10 Kết nối tri thức
Giải mục 1 trang 25 SGK Toán 10 tập 2 - Kết nối tri thức Giải mục 2 trang 25, 26 SGK Toán 10 tập 2 - Kết nối tri thức Giải bài 6.20 trang 27 SGK Toán 10 – Kết nối tri thức Giải bài 6.21 trang 27 SGK Toán 10 – Kết nối tri thức Giải bài 6.22 trang 27 SGK Toán 10 – Kết nối tri thức Giải bài 6.23 trang 27 SGK Toán 10 – Kết nối tri thứcLý thuyết Phương trình quy về phương trình bậc hai - SGK Toán 10 Kết nối tri thức
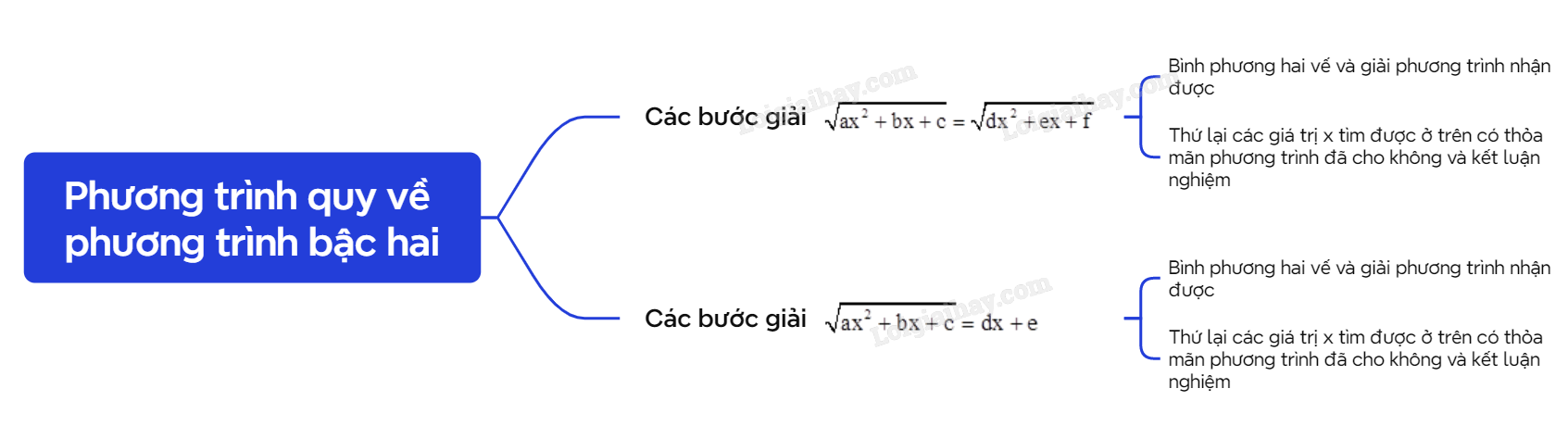
A. Lý thuyết 1. Phương trình dạng √ax2+bx+c=√dx2+ex+f
A. Lý thuyết
1. Phương trình dạng √ax2+bx+c=√dx2+ex+f
|
Để giải phương trình √ax2+bx+c=√dx2+ex+f, ta thực hiện như sau: - Bình phương hai vế và giải phương trình nhận được. - Thứ lại các giá trị x tìm được ở trên có thỏa mãn phương trình đã cho không và kết luận nghiệm. |
2. Phương trình dạng √ax2+bx+c=dx+e
|
Để giải phương trình √ax2+bx+c=dx+e, ta thực hiện như sau: - Bình phương hai vế và giải phương trình nhận được. - Thứ lại các giá trị x tìm được ở trên có thỏa mãn phương trình đã cho không và kết luận nghiệm. |
B. Bài tập
Bài 1: Giải phương trình √2x2−4x−2=√x2−x−2.
Giải:
Bình phương hai vế của phương trình, ta được 2x2−4−2=x2−x−2.
Sau khi thu gọn, ta được x2−3x=0. Từ đó tìm được x = 0 hoặc x = 3.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 3 thỏa mãn.
Vậy nghiệm của phương trình đã cho là x = 3.
Bài 2: Giải phương trình √2x2−5x−9=x−1.
Giải:
Bình phương hai vế của phương trình, ta được 2x2−5x−9=x2−2x+1.
Sau khi thu gọn, ta được x2−3x−10=0. Từ đó tìm được x = -2 hoặc x = 5.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 5 thỏa mãn.
Vậy nghiệm của phương trình đã cho là x = 5.

Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365