Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm Toán 10 Cánh diều
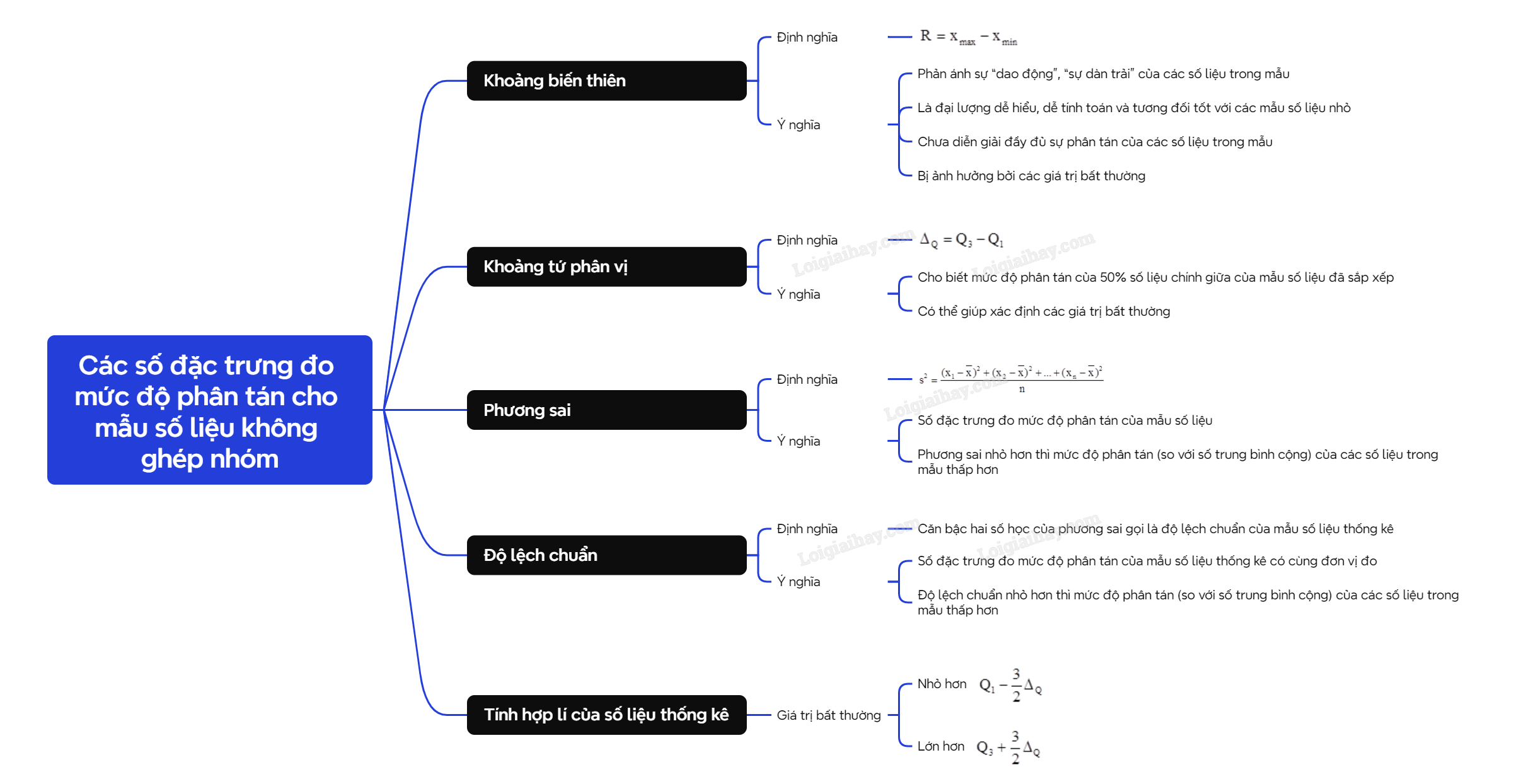
A. Lý thuyết 1. Khoảng biến thiên, khoảng tứ phân vị a) Định nghĩa
A. Lý thuyết
1. Khoảng biến thiên, khoảng tứ phân vị
a) Định nghĩa
|
- Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó. Ta có thể tính khoảng biến thiên R của mẫu số liệu theo công thức sau: R=xmax−xmin, trong đó xmax là giá trị lớn nhất, xmin là giá trị nhỏ nhất của mẫu số liệu đó. - Giả sử Q1, Q2, Q3 là tứ phân vị của mẫu số liệu. Ta gọi hiệu ΔQ=Q3−Q1 là khoảng tứ phân vị của mẫu số liệu đó. |
b) Ý nghĩa
- Khoảng biến thiên:
+ Phản ánh sự “dao động”, “sự dàn trải” của các số liệu trong mẫu.
+ Là đại lượng dễ hiểu, dễ tính toán và tương đối tốt với các mẫu số liệu nhỏ.
+ Chưa diễn giải đầy đủ sự phân tán của các số liệu trong mẫu.
+ Bị ảnh hưởng bởi các giá trị bất thường.
- Khoảng tứ phân vị:
+ Cho biết mức độ phân tán của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp.
+ Có thể giúp xác định các giá trị bất thường.
2. Phương sai
a) Định nghĩa
|
Cho mẫu số liệu thống kê có n giá trị x1,x2,...,xn và số trung bình cộng là ¯x. Ta gọi số s2=(x1−¯x)2+(x2−¯x)2+...+(xn−¯x)2n là phương sai của mẫu số liệu trên. |
b) Ý nghĩa
Phương sai là số đặc trưng đo mức độ phân tán của mẫu số liệu. Mẫu số liệu nào có phương sai nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn.
3. Độ lệch chuẩn
a) Định nghĩa
| Căn bậc hai số học của phương sai gọi là độ lệch chuẩn của mẫu số liệu thống kê. |
Nhận xét: Vì độ lệch chuẩn có cùng đơn vị đo với số liệu thống kê nên khi cần chú ý đến đơn vị đo thì ta sử dụng độ lệch chuẩn mà không sử dụng phương sai.
b) Ý nghĩa
Cũng như phương sai, khi hai mẫu số liệu thống kê có cùng đơn vị đo và có số trung bình cộng bằng nhau (hoặc xấp xỉ nhau), mẫu số liệu nào có độ lệch chuẩn nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn. Độ lệch chuẩn là số đặc trưng đo mức độ phân tán của mẫu số liệu thống kê có cùng đơn vị đo.
4. Tính hợp lí của số liệu thống kê
Ta có thể sử dụng các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm để chỉ ra được những số liệu bất thường của mẫu số liệu đó. Ta thường sử dụng khoảng tứ phân vị để xác định số liệu bất thường của mẫu số liệu. Cụ thể như sau:
|
Giả sử Q1, Q2, Q3 là tứ phân vị của mẫu số liệu và hiệu ΔQ=Q3−Q1 là khoảng tứ phân vị của mẫu số liệu đó. Một giá trị của mẫu số liệu được coi là một giá trị bất thường nếu nó nhỏ hơn Q1−32ΔQ hoặc lớn hơn Q3+32ΔQ. |
B. Bài tập
Bài 1: Mẫu số liệu thống kê chiều cao (đơn vị: mét) của 15 cây bạch đàn là:
6,3 6,6 8,2 8,3 7,8 7,9 9,0 8,9 7,2 7,5 8,7 7,7 8,8 7,6
a) Tìm khoảng biến thiên của mẫu số liệu.
b) Tìm khoảng tứ phân vị của mẫu số liệu.
Giải:
a) Trong mẫu số liệu, số lớn nhất là 9,0 và số bé nhất là 6,3. Vậy khoảng biến thiên của mẫu số liệu là:
R=xmax−xmin=9,0−6,3=2,7 (m).
b) Sắp xếp các số liệu của mẫu theo thứ tự không giảm, ta được:
6,3 6,6 7,2 7,5 7,5 7,6 7,7 7,8 7,9 8,2 8,3 8,7 8,8 8,9 9,0
Do đó Q1=7,5 (m); Q2=7,8 (m); Q3=8,7 (m).
Vậy khoảng tứ phân vị của mẫu số liệu là:
ΔQ=Q3−Q1=8,7−7,5=1,2 (m).
Bài 2: Bảng dưới đây thống kê nhiệt độ (đơn vị: oC) ở Thành phố Hồ Chí Minh ngày 3/6/2021 sau một số lần đo.

Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu trên.
Giải:
Nhiệt độ trung bình là:
¯x=27+26+28+32+34+35+30+288=30 (oC).
Phương sai của mẫu số liệu là:
s2=(x1−¯x)2+(x2−¯x)2+(x3−¯x)2+(x4−¯x)2+(x5−¯x)2+(x6−¯x)2+(x7−¯x)2+(x8−¯x)2n
=(−3)2+(−4)2+(−2)2+22+42+52+02+(−2)28=788=9,75.
Độ lệch chuẩn của mẫu số liệu đó là: s=√9,75≈3,12 (oC).
Bài 3: Nếu các giá trị bất thường của mẫu số liệu thống kê sau:
5 6 19 21 22 23 24 25 26 27 28 29 30 31 32 33 34 48 49
Giải:
Mẫu số liệu có tứ phân vị là Q1=22, Q2=27, Q3=32.
Suy ra ΔQ=Q3−Q1=32−22=10.
Ta có Q1−32ΔQ=22−32.10=7, Q3+32ΔQ=32+32.10=47.
Vậy các giá trị 5, 6 (nhỏ hơn 7) và 48, 49 (lớn hơn 47) là các giá trị bất thường của mẫu số liệu.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365