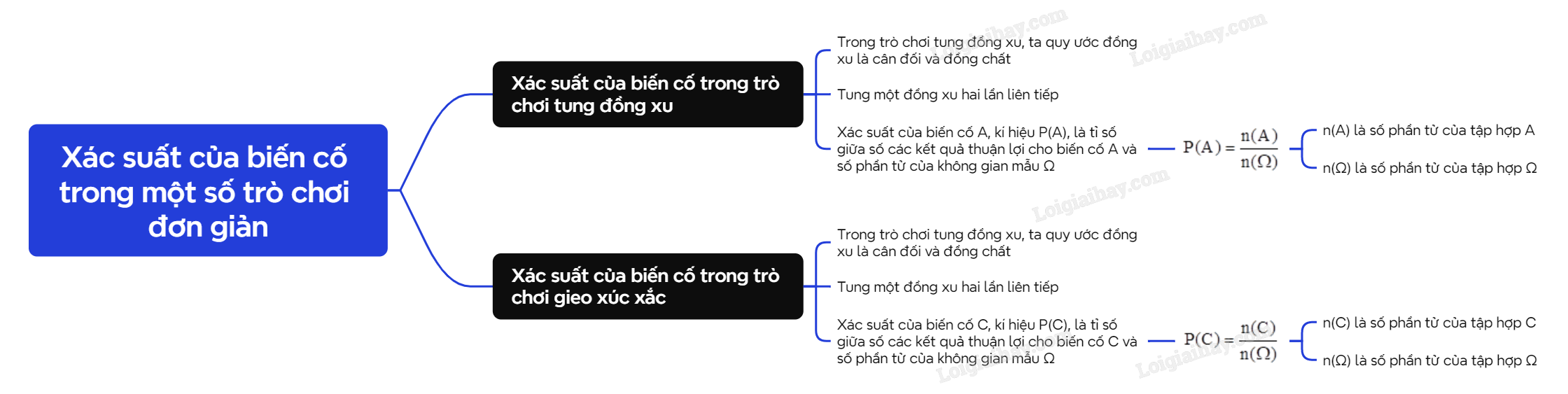
A. Lý thuyết

1. Xác suất của biến cố trong trò chơi tung đồng xu

Trong trò chơi tung đồng xu, ta quy ước đồng xu là cân đối và đồng chất.

Tung một đồng xu hai lần liên tiếp.

- Tập hợp Ω các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu sau hai lần tung là Ω = {SS; SN; NS; NN}, trong đó, chẳng hạn SN là kết quả “Lần thứ nhất đồng xu xuất hiện mặt sấp, lần thứ hai đồng xu xuất hiện mặt ngửa”. 

- Tập hợp Ω gọi là không gian mẫu trong trò chơi tung một đồng xu hai lần liên tiếp.

Xét sự kiện “Kết quả của hai lần tung đồng xu là giống nhau”.

- Tập hợp A các kết quả có thể xảy ra với sự kiện trên là A = {SS; NN}. Ta thấy \(A \subset \Omega \). Tập hợp A còn gọi là biến cố ngẫu nhiên (hay gọi tắt là biến cố) trong trò chơi này. Khi đó, sự kiện đã nêu chỉ ra tính chất đặc trưng cho các phần tử của tập hợp A. 

- Mỗi phần tử của tập hợp A được gọi là một kết quả thuận lợi cho biến cố A: “Kết quả của hai lần tung đồng xu là giống nhau”.

Trong trò chơi tung một đồng xu hai lần liên tiếp, đối với mỗi biến cố A, ta có định nghĩa cổ điển của xác suất như sau:

2. Xác suất của biến cố trong trò chơi gieo xúc xắc

Trong trò chơi gieo xúc xắc, ta quy ước xúc xắc là cân đối và đồng chất.

Gieo một xúc xắc hai lần liên tiếp.

Khi gieo một xúc xắc hai lần liên tiếp, có 36 kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc sau hai lần gieo, đó là:

(1;1)  (1;2)  (1;3)  (1;4)  (1;5)  (1;6)  (1;1)  (1;2)  (1;3)  (1;4)  (1;5)  (1;6)
(2;1)  (2;2)  (2;3)  (2;4)  (2;5)  (2;6)  (2;1)  (2;2)  (2;3)  (2;4)  (2;5)  (2;6)
(3;1)  (3;2)  (3;3)  (3;4)  (3;5)  (3;6)  (3;1)  (3;2)  (3;3)  (3;4)  (3;5)  (3;6)
(4;1)  (4;2)  (4;3)  (4;4)  (4;5)  (4;6)  (4;1)  (4;2)  (4;3)  (4;4)  (4;5)  (4;6)
(5;1)  (5;2)  (5;3)  (5;4)  (5;5)  (5;6)  (5;1)  (5;2)  (5;3)  (5;4)  (5;5)  (5;6)
(6;1)  (6;2)  (6;3)  (6;4)  (6;5)  (6;6)  (6;1)  (6;2)  (6;3)  (6;4)  (6;5)  (6;6)

- Tập hợp Ω các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc sau hai lần gieo là Ω = {(i; j) ∣ i, j = 1, 2, 3, 4, 5, 6}, trong đó (i; j) là kết quả “Lần thứ nhất xuất hiện mặt i chấm, lần thứ hai xuất hiện mặt j chấm”.

- Tập hợp Ω gọi là không gian mẫu trong trò chơi gieo một xúc xắc hai lần liên tiếp.

Xét sự kiện “Tổng số chấm trong hai lần gieo xúc xắc bằng 8”.

- Tập hợp C các kết quả có thể xảy ra đối với sự kiện trên là:

C ={(2; 6); (3; 5); (4; 4); (5; 3); (6; 2)}.

Ta thấy \(C \subset \Omega \). Tập hợp C cũng gọi là biến cố ngẫu nhiên (hay gọi tắt là biến cố) trong trò chơi nói trên. Khi đó, sự kiện đã nêu chỉ ra tính chất đặc trưng cho các phần tử của tập hợp C.

- Mỗi phần tử của tập hợp C được gọi là một kết quả thuận lợi cho biến cố C: “Tổng số chấm trong hai lần gieo xúc xắc bằng 8”.

Trong trò chơi gieo một xúc xắc hai lần liên tiếp, đối với mỗi biến cố C, ta có định nghĩa cổ điển của xác suất như sau:

B. Bài tập

Bài 1: Tung một đồng xu hai lần liên tiếp.

a) Tính n(Ω) với Ω là không gian mẫu trong trò chơi trên.

b) Xét biến cố B: “Có ít nhất một lần xuất hiện mặt ngửa”.
Tính xác suất của biến cố BB.

Giải:

a) Không gian mẫu trong trò chơi trên là tập hợp Ω = {SS; SN; NS; NN}. Do đó, n(Ω) = 4.

b) Các kết quả thuận lợi cho biến cố B là: SN, NS, NN, tức là B = {SN; NS; NN}.

Vì thế, n(B) =3. Vậy xác suất của biến cố B là: \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{3}{4}\).

Bài 2: Gieo một xúc xắc hai lần liên tiếp.

a) Tính n(Ω) với Ω là không gian mẫu trong trò chơi trên.

b) Xét biến cố D: “Số chấm trong hai lần gieo đều là số lẻ”. Tính xác suất của biến cố D.

Giải:

a) Không gian mẫu trong trò chơi trên là tập hợp Ω = {(i; j) ∣ i, j = 1, 2, 3, 4, 5, 6},
trong đó (i; j) là kết quả “Lần đầu xuất hiện mặt i chấm, lần sau xuất hiện mặt j chấm”. Vậy n(Ω) = 36.

b) Các kết quả thuận lợi cho biến cố D là: (1; 1); (1; 3); (1; 5); (3; 1); (3; 3); (3; 5); (5; 1); (5; 3); (5; 5), tức là D = {(1; 1); (1; 3); (1; 5); (3; 1); (3; 3); (3; 5); (5; 1); (5; 3); (5; 5)}.

Vậy xác suất của biến cố D là: \(P(D) = \frac{{n(D)}}{{n(\Omega )}} = \frac{9}{{36}} = \frac{1}{4}\).