Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 25. Nhị thức Newton Toán 10 Kết nối tri thức
Lý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
Giải mục 1 trang 72, 73, 74 SGK Toán 10 tập 2 - Kết nối tri thức Giải bài 8.12 trang 74 SGK Toán 10 – Kết nối tri thức Giải bài 8.13 trang 74 SGK Toán 10 – Kết nối tri thức Giải bài 8.14 trang 74 SGK Toán 10 – Kết nối tri thức Giải bài 8.15 trang 75 SGK Toán 10 – Kết nối tri thức Giải bài 8.16 trang 75 SGK Toán 10 – Kết nối tri thứcLý thuyết Nhị thức Newton - SGK Toán 10 Kết nối tri thức
1. Một số công thức khai triển
A. Lý thuyết
1. Một số công thức khai triển
|
(a+b)4=C04a4+C14a3b+C24a2b2+C34a1b3+C44b4=a4+4a3b+6a2b2+4a1b3+b4.
(a+b)5=C05a5+C15a4b+C25a3b2+C35a2b3+C45ab4+C55b5 =a5+5a4b+10a3b2+10a2b3+5ab4+b5. |
Những công thức khai triển nói trên là công thức nhị thức Newton (a+b)n ứng với n = 4 và n = 5.
Chú ý: Các hệ số trong khai triển nhị thức Newton (a+b)n với n = 0; 1; 2; 3;… được viết thành từng hàng và xếp thành bảng số dưới đây. Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của hai số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũ tên trên bảng). Bảng số này được gọi là tam giác Pascal.
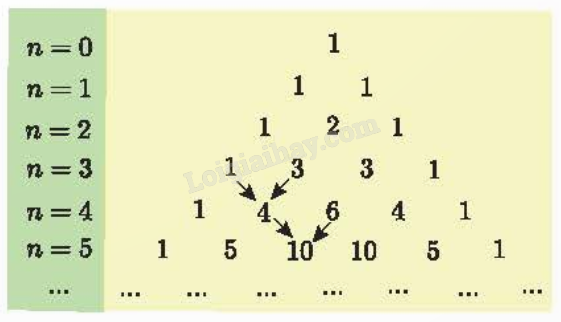
2. Công thức khai triển tổng quát
| (a+b)n=C0nan+C1nan−1b+...+Cknan−kbk+...+Cn−1nabn−1+Cnnbn. |
Nhận xét:
- Số hạng tổng quát trong khai triển của (a+b)n đều có dạng Cknan−kbk (0≤k≤n).
- Từ công thức nhị thức Newton nói trên, ta có khai triển của (a−b)n như sau:
(a−b)n=C0nan−C1nan−1b+C2nan−2b2−C3nan−3b3+..., ở đó các dấu “+”, “-“ xen kẽ nhau.
Ví dụ: (a−b)3=C03a3−C13a3−1b+C23a3−2b2−C33a3−3b3=C03a3−C13a2b+C23ab2−C33b3.
Có thể xem thêm trong chuyên đề học tập Toán 10.
B. Bài tập
Bài 1: Khai triển biểu thức (x+1)4.
Giải:
Xác định số hạng: a = x, b = 1.
(x+1)4=C04x4+C14x3.1+C24x2.12+C34x1.13+C44.14=a4+4x3+6x2+4x+1.
Bài 2: Khai triển biểu thức (x−1)4.
Giải:
Có hai cách khai triển, tùy thuộc vào việc đặt b = -1 hay b = 1.
Nếu coi a = x, b = -1:
(x−1)4=C04x4+C14x3.(−1)+C24x2.(−1)2+C34x1.(−1)3+C44.(−1)4=a4−4x3+6x2−4x+1.
Hoặc có thể coi a = x, b = 1 và áp dụng công thức khai triển tổng quát:
(a−b)n=C0nan−C1nan−1b+C2nan−2b2−C3nan−3b3+..., khi đó sẽ nhận được kết quả như trên (xen kẽ dấu).
Bài 3:
a) Khai triển biểu thức (x−2y)4 và tìm hệ số của số hạng chứa y4.
b) Khai triển biểu thức (3x−y)5.
Giải:
a) Coi a = x, b = -2y.
(x−2y)4=[x+(−2y)]4=x4+4x3(−2y)+6x2(−2y)2+4x(−2y)3+(−2y)4
=x4−8x3y+24x2y2−32xy3+16y4.
Số hạng chứa y4 là 16y4, hệ số là 16.
b) Coi a = 3x, b = -y.
(3x−y)5=[3x+(−y)]5
=(3x)5+5.(3x)4.(−y)+10(3x)3.(−y)2+10(3x)2.(−y)3+5.(3x).(−y)4+(−y)5
=243x5−405x4y+270x3y2−90x2y3+15xy4−y5.
Bài 4:
a) Xác định hệ số của x6 trong khai triển (2x+1)12.
b) Xác định hệ số của x9 trong khai triển (3x−2)18.
Giải:
a) Số hạng chứa x6 là C612.(2x)6=C612.26x6. Hệ số của x6 là C612.26.
b) Số hạng chứa x9 là C918.(3x)9.(−2)9=C918.(−2)939x9=−C918.2939x9. Hệ số của x9 là −C918.2939=−C918.69.
Bài 5: Cho tập hợp A = { a; b; c; d; e }. Tập hợp A có bao nhiêu tập hợp con?
Giải:
Tập hợp A có 5 phần tử. Mỗi tập con của A có k phần tử (1 ≤ k ≤ 5) là một tổ hợp chập k của A. Do đó, số tập con như vậy bằng Ck5. Mặt khác, có một tập con của A không có phần tử nào (tập rỗng), tức có C05=1 tập con như vậy. Do đó, số tập con của A bằng C05+C15+C25+C35+C45+C55.
Theo công thức nhị thức Newton, ta có C05+C15+C25+C35+C45+C55=(1+1)5=25.
Vậy A có 25=32 tập con.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365