Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 5. Phương trình và bất phương trình lôgarit Toán 11 Cùng khám phá
Lý thuyết Phương trình và bất phương trình logarit - SGK Toán 11 Cùng khám phá
Giải mục 1 trang 24, 25 SGK Toán 11 tập 2 - Cùng khám phá Giải mục 2 trang 25, 26 SGK Toán 11 tập 2 - Cùng khám phá Bài 6.17 trang 26 SGK Toán 11 tập 2 - Cùng khám phá Bài 6.18 trang 26 SGK Toán 11 tập 2 - Cùng khám phá Bài 6.19 trang 26 SGK Toán 11 tập 2 - Cùng khám pháLý thuyết Phương trình và bất phương trình logarit - SGK Toán 11 Cùng khám phá
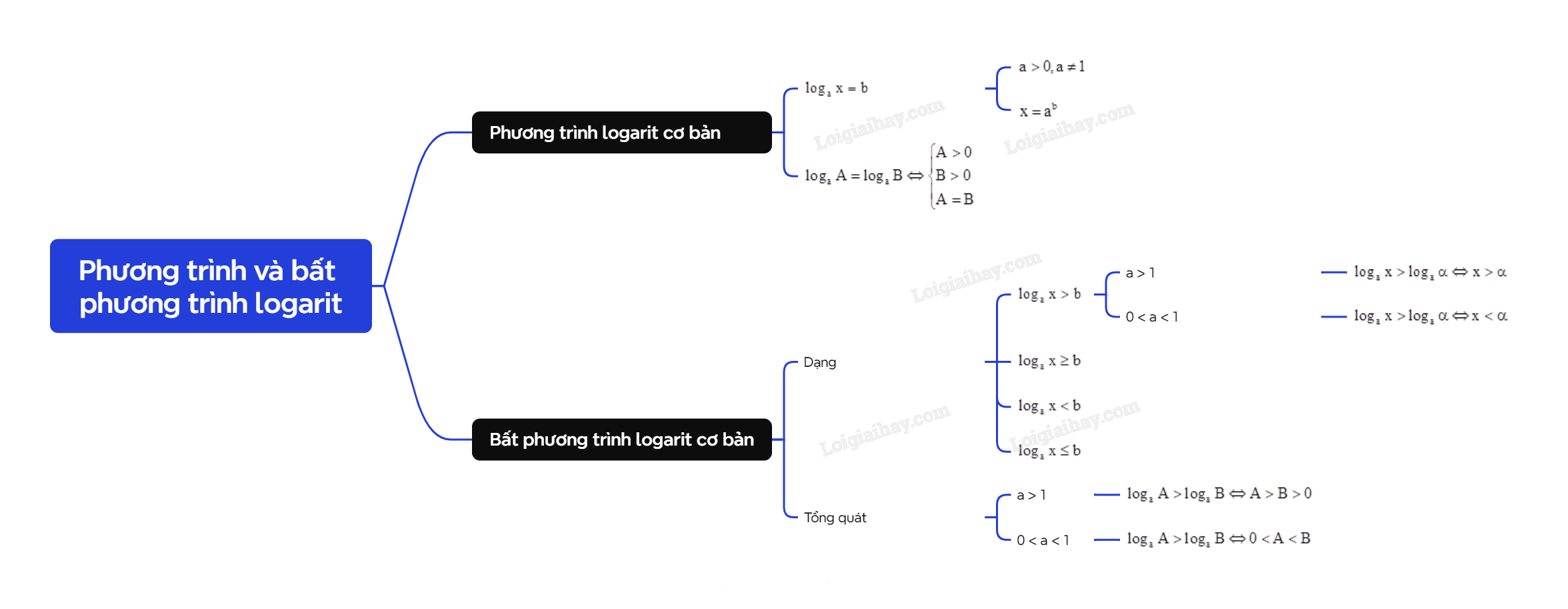
1. Phương trình logarit cơ bản Phương trình mũ cơ bản có
A. Lý thuyết
1. Phương trình logarit cơ bản
Phương trình mũ cơ bản có dạng logax=blogax=b (a>0,a≠1)(a>0,a≠1).
| Phương trình logax=blogax=b (a>0,a≠1)(a>0,a≠1) luôn có nghiệm duy nhất x=abx=ab với mọi b. |
Lưu ý: Nếu b=logaαb=logaα (α>0)(α>0) thì phương trình logax=blogax=b trở thành logax=logaαlogax=logaα với mọi b. Khi đó, phương trình có nghiệm duy nhất x=αx=α. Một cách tổng quát, với a > 0 và a≠1a≠1 , ta có:
logaA=logaB⇔{A>0B>0A=B.
2. Bất phương trình logarit cơ bản
Bất phương trình mũ cơ bản có dạng logax>b hoặc logax≥b, logax<b, logax≤b (a>0,a≠1).
|
Cho bất phương trình logax>b (a>0,a≠1): - Nếu a > 1: Ta có logax>b⇔x>ab. - Nếu 0 < a < 1: Ta có logax>b⇔0<x<ab. |
Lưu ý:
Giải tương tự cho các trường hợp còn lại: logax≥b, logax<b, logax≤b.
Nếu b=logaα (α>0) thì bất phương trình logax>b trở thành logax>logaα. Khi đó:
- Nếu a > 1 thì logax>logaα⇔x>α.
- Nếu 0 < a < 1 thì logax>logaα⇔x<α.
Một cách tổng quát, ta có:
- Khi a > 1 thì logaA>logaB⇔A>B>0.
- Khi 0 < a < 1 thì logaA>logaB⇔0<A<B.
B. Bài tập
Bài 1: Giải các phương trình:
a) log2(x+1)=3.
b) ln(x+1)=ln(x2−1).
Giải:
a) Điều kiện của phương trình là x+1>0⇔x>−1.
Ta có log2(x+1)=3⇔x+1=23⇔x+1=8⇔x=7.
Vậy phương trình có nghiệm duy nhất x = 7.
b) Điều kiện của phương trình là {x+1>0x2−1>0⇔{x>−1[x<−1x>1⇔x>1.
Ta có ln(x+1)=ln(x2−1)⇒x+1=x2−1.
x+1=x2−1⇔x2−x−2=0⇔[x=−1x=2.
Kết hợp với điều kiện của phương trình, ta loại x = -1 và nhận x = 2.
Vậy phương trình có nghiệm duy nhất x = 2.
Bài 2: Giải các bất phương trình:
a) log2x>7.
b) log0,5(6x+12)<log0,5(x2+7x+10).
Giải:
a) Vì cơ số 2 lớn hơn 1 nên log2x>7⇔x>27⇔x>128.
Vậy tập nghiệm của bất phương trình là (128;+∞).
b) Điều kiện của bất phương trình là {6x+12>0x2+7x+10>0⇔{x>−2[x<−5x>−2⇔x>−2.
Vì cơ số 0,5 nhỏ hơn 1 nên log0,5(6x+12)<log0,5(x2+7x+10)⇔6x+12>x2+7x+10⇔x2+x−2<0⇔−2<x<1.
Kết hợp điều kiện, ta được tập nghiệm của bất phương trình là (−2;1).
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365