1. Hệ thức về cạnh và đường cao trong tam giác vuông 

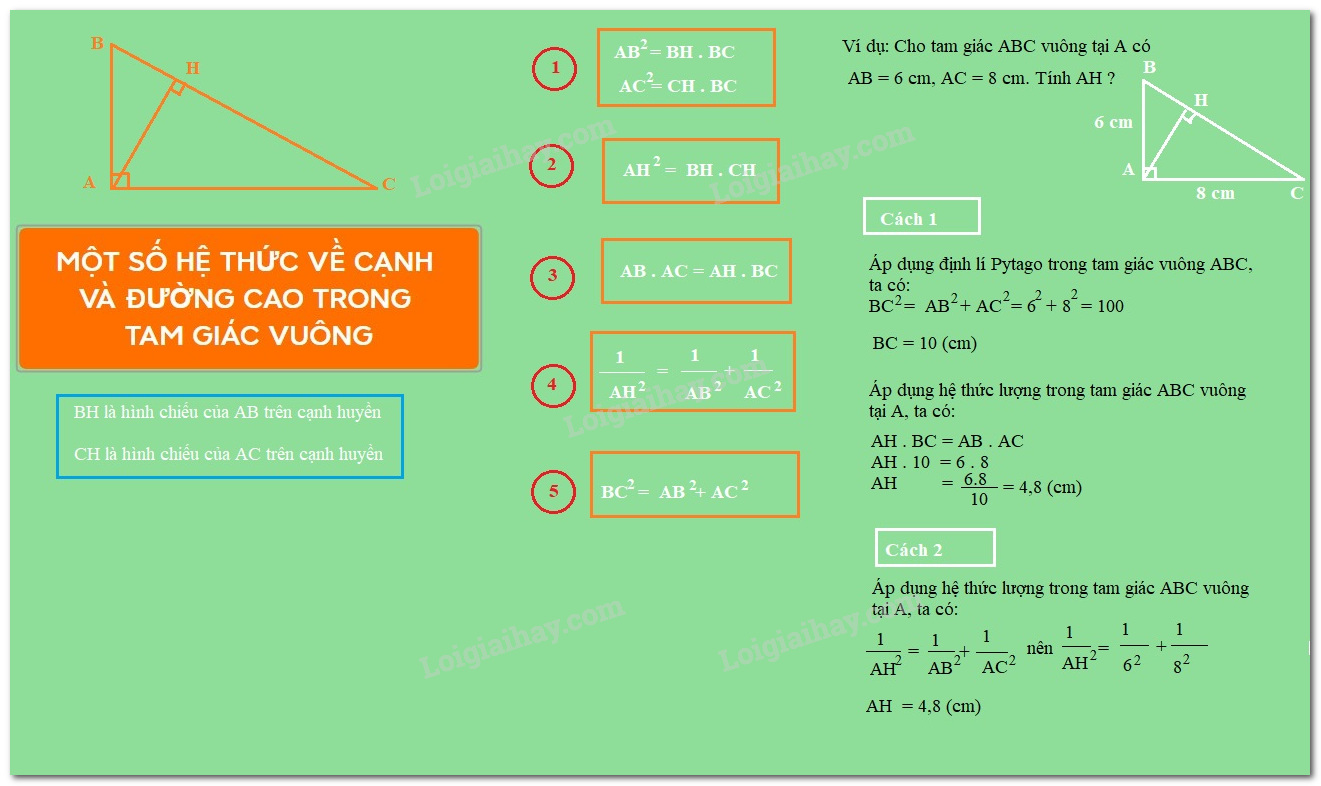
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ (hình vẽ). Khi đó ta có các hệ thức sau:

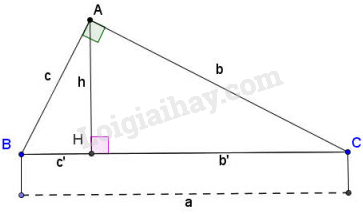
+) $A{B^2} = BH.BC$ và $A{C^2} = CH.BC$ hay ${c^2} = a.c'$ và ${b^2} = ab'$ (1)

+) $H{A^2} = HB.HC$ hay ${h^2} = c'b'$ (2)

+) $AB.AC = BC.AH$ hay $cb = ah$ (3)

+) $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$ hay $\dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{b^2}}}$ (4).

+) $B{C^2} = A{B^2} + A{C^2}$ (Định lí Pitago). 

2. Các dạng toán cơ bản

Dạng 1: Tính độ dài các đoạn thẳng trong tam giác vuông

Phương pháp:

Sử dụng hệ thức về cạnh và đường cao trong tam giác vuông.

Dạng 2: Chứng minh các hệ thức liên quan giữa các yếu tố trong tam giác vuông

Phương pháp:

Ta thường sử dụng các kiến thức:

- Đưa về hai tam giác đồng dạng có chứa các đoạn thẳng có trong hệ thức.

- Sử dụng các hệ thức về cạnh và đường cao trong tam giác vuông để chứng minh.

baitap365.com