Mô phỏng lí thuyết: Tổng và hiệu của hai vecto

1. Tổng của hai vectơ

Định nghĩa: Cho hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$. Lấy một điểm $A$ tùy ý, vẽ $\overrightarrow{AB}$ = $\overrightarrow{a}$, $\overrightarrow{BC}$ = $\overrightarrow{b}$. Vectơ $\overrightarrow{AC}$ được gọi là tổng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$.

$\overrightarrow{AC}$ = $\overrightarrow{a}$ + $\overrightarrow{b}$.

2. Quy tắc hình bình hành 

Nếu $ABCD$ là hình bình hành thì 

$\overrightarrow{AB}$ + $\overrightarrow{AD}$ = $\overrightarrow{AC}$.

3. Tính chất của tổng các vectơ

- Tính chất giao hoán

$\overrightarrow{a}$ + $\overrightarrow{b}$ = $\overrightarrow{b}$ + $\overrightarrow{a}$

- Tính chất kết hợp

($\overrightarrow{a}$ + $\overrightarrow{b}$ ) + $\overrightarrow{c}$ = $\overrightarrow{a}$ + ($\overrightarrow{b}$ +$\overrightarrow{c}$)

- Tính chất của $\overrightarrow{0}$:

$\overrightarrow{a}$+$\overrightarrow{0}$ = $\overrightarrow{0}$ + $\overrightarrow{a}$ $=\overrightarrow{a}$

4. Hiệu của hai vectơ

a) Vec tơ đối: Vectơ có cùng độ dài và ngược hướng với vec tơ $\overrightarrow{a}$ được gọi là vec tơ đối của vec tơ $\overrightarrow{a}$, kí hiệu $-\overrightarrow{a}$.

Vec tơ đối của $\overrightarrow{0}$ là vectơ $\overrightarrow{0}$.

b) Hiệu của hai vec tơ: Cho hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$. Vec tơ hiệu của hai vectơ, kí hiệu $\overrightarrow{a}$- $\overrightarrow{b}$ là vectơ $\overrightarrow{a}$ + (-$\overrightarrow{b}$)

                  $\overrightarrow{a}$- $\overrightarrow{b}$ = $\overrightarrow{a}$ + (-$\overrightarrow{b}$).

c) Chú ý: Với ba điểm bất kì, ta luôn có 

                  $\overrightarrow{AB}$ + $\overrightarrow{BC}$ = $\overrightarrow{AC}$           (1)

                   $\overrightarrow{AB}$ - $\overrightarrow{AC}$ = $\overrightarrow{CB}$             (2)

(1) là quy tắc 3 điểm (quy tắc tam giác) đối với tổng của hai vectơ.

(2) là quy tắc 3 điểm (quy tắc tam giác) đối với hiệu các vectơ.

5. Áp dụng 

a) Trung điểm của đoạn thẳng:

$I$ là trung điểm của đoạn thẳng

⇔  $\overrightarrow{IA}$ +$\overrightarrow{IB}$ = $\overrightarrow{0}$

b) Trọng tâm của tam giác:

$G$ là trọng tâm  của tam giác ∆ABC 

⇔ $\overrightarrow{GA}$ + $\overrightarrow{GB}$+$\overrightarrow{GC}$ = $\overrightarrow{0}$

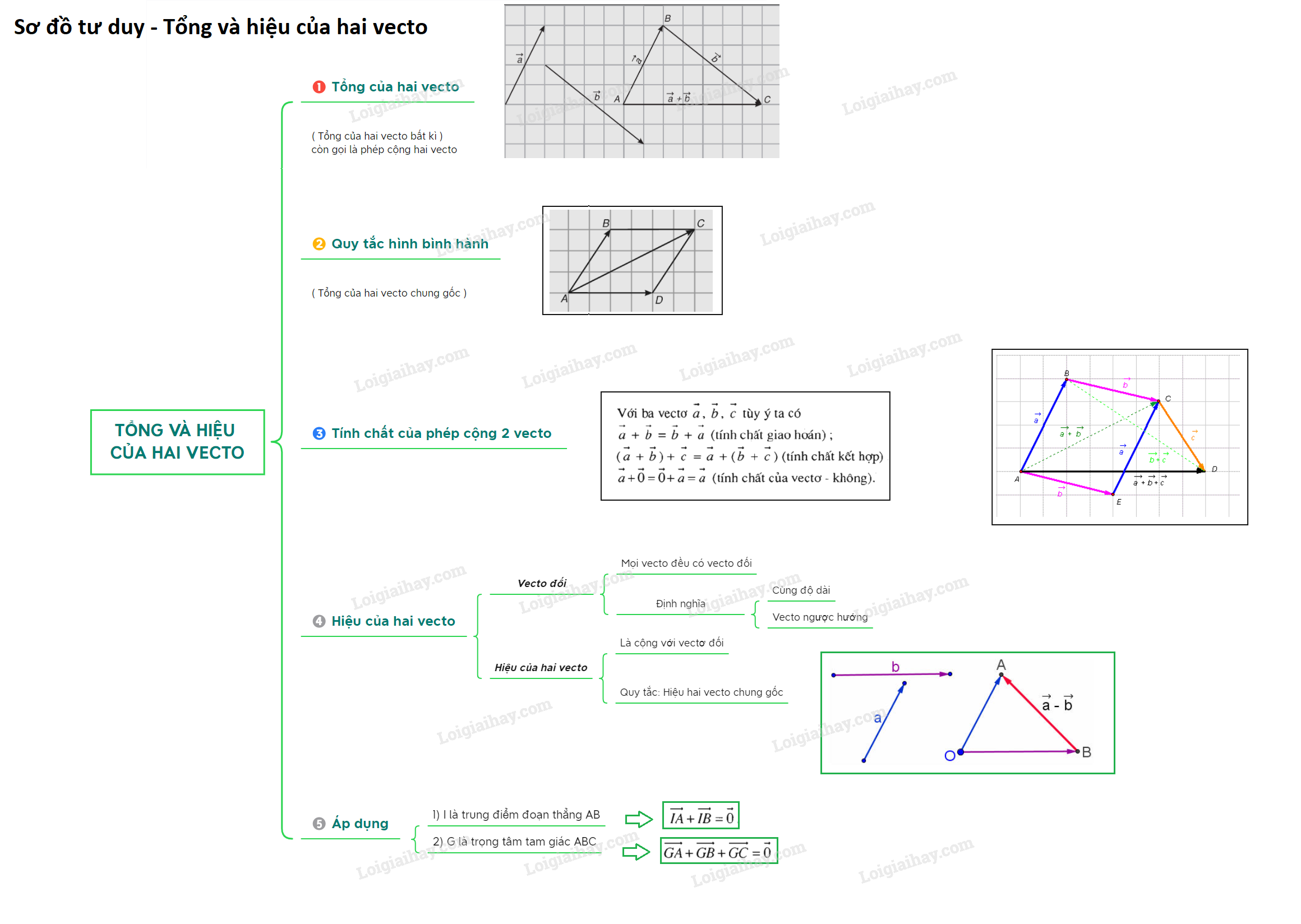
Sơ đồ tư duy - Tổng và hiệu của hai vecto

baitap365.com