Đề bài

a) Tính $x = \cos \dfrac{{2\pi }}{5}$ bằng “phương pháp hình học” như sau:

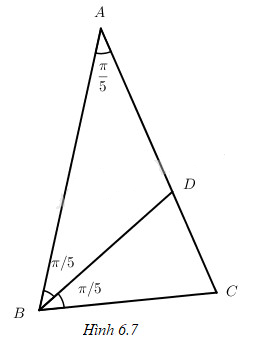
Xét tam giác cân ABC với $\widehat B = \widehat C = \dfrac{{2\pi }}{5}$, kẻ đường phân giác BD của tam giác đó. Từ tính chất  $\dfrac{{BC}}{{BA}} = \dfrac{{DC}}{{DA}}$ (h. 6.7) hãy suy ra $4{x^2} + 2x - 1 = 0$.

b) Từ đó tính $\cos \dfrac{\pi }{5},\sin \dfrac{\pi }{5},\tan \dfrac{\pi }{5}$.

c) Tính sin, côsin, tang của ${18^0}$

d) Viết $6 = 36 - 30$, tính sin, côsin của ${6^0}$. Thử lại bằng má tính bỏ túi.