Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 8. Quan hệ chia hết và tính chất
Lý thuyết Quan hệ chia hết và tính chất Toán 6 KNTT với cuộc sống
Trả lời Câu hỏi 1 trang 30 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Câu hỏi 2 trang 30 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Hoạt động 1 trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Hoạt động 2 trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Luyện tập 1 trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Thử thách nhỏ trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Hoạt động 3 trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Hoạt động 4 trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Luyện tập 2 trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Vận dụng 1 trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Hoạt động 5 trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Hoạt động 6 trang 31 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Luyện tập 3 trang 32 SGK Toán 6 Kết nối tri thức với cuộc sống Trả lời Vận dụng 2 trang 32 SGK Toán 6 Kết nối tri thức với cuộc sống Giải Bài 2.1 trang 33 SGK Toán 6 Kết nối tri thức với cuộc sống tập 1 Giải Bài 2.2 trang 33 SGK Toán 6 Kết nối tri thức với cuộc sống tập 1 Giải Bài 2.3 trang 33 SGK Toán 6 Kết nối tri thức với cuộc sống tập 1 Giải Bài 2.4 trang 33 SGK Toán 6 Kết nối tri thức với cuộc sống tập 1 Giải Bài 2.5 trang 33 SGK Toán 6 Kết nối tri thức với cuộc sống tập 1 Giải Bài 2.6 trang 33 SGK Toán 6 Kết nối tri thức với cuộc sống tập 1 Giải Bài 2.7 trang 33 SGK Toán 6 Kết nối tri thức với cuộc sống tập 1 Giải Bài 2.8 trang 33 SGK Toán 6 Kết nối tri thức với cuộc sống tập 1 Giải Bài 2.9 trang 33 SGK Toán 6 Kết nối tri thức với cuộc sống tập 1 Các dạng toán về quan hệ chia hết và tính chấtLý thuyết Quan hệ chia hết và tính chất Toán 6 KNTT với cuộc sống
Lý thuyết Quan hệ chia hết và tính chất Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
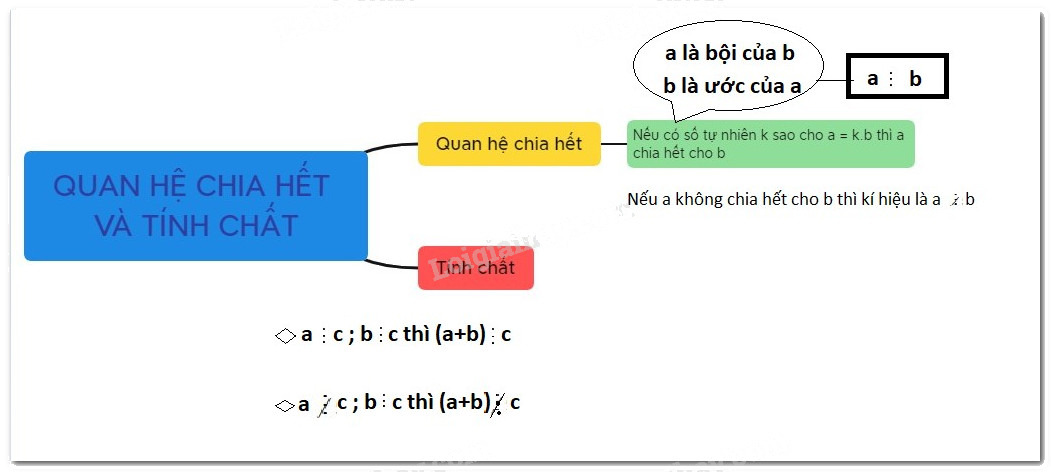
1. Quan hệ chia hết
Khi nào thì a chia hết cho b?
Cho hai số tự nhiên a và b, trong đó b≠0, nếu có số tự nhiên x sao cho b.x=a thì ta nói a chia hết cho b và ta có phép chia hết a:b=x
Nếu a không chia hết cho b, ta kí hiệu là a⋮̸b.
Ước và bội
- Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.
- Kí hiệu: Ư(a) là tập hợp các ước của a và B(b) là tập hợp các bội của b.
Ví dụ : 12⋮6⇒12 là bội của 6. Còn 6 được gọi là ước của 12
Cách tìm ước và bội
Tìm ước:
- Ta có thể tìm các ước của a(a>1) bằng cách lần lượt chia a cho các số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
Ví dụ :
16:1=16; 16:2=8; 16:4=4; 16:8=2; 16:16=1
Vậy các ước của 16 là 1;2;4;8;16. Tập hợp các ước của 16 là:
Ư(16)={1;2;4;8;16}
Tìm bội:
- Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lượt với 0,1,2,3,...
Ví dụ :
Ta lấy 6 nhân với từng số 0 thì được 0 nên 0 là bội của 6, lấy 6.1=6 nên 6 là bội của 6, 6.2=12 nên 12 là bội của 6,...
Vậy B(6)={0;6;12;18;...}
2. Tính chất chia hết của một tổng
- Tính chất 1: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
a⋮m và b⋮m ⇒(a+b)⋮m
a⋮m;b⋮m;c⋮m⇒(a+b+c)⋮m
- Tính chất 2: Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.
a⋮m và b⋮̸m⇒(a+b)⋮̸m
a⋮̸m;b⋮m;c⋮m⇒(a+b+c)⋮̸m
Ví dụ: Ta có 6⋮3;9⋮3;15⋮3⇒6+9+15=30⋮3;10⋮5;15⋮5;12⋮̸5⇒10+15+12=37⋮̸5
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365