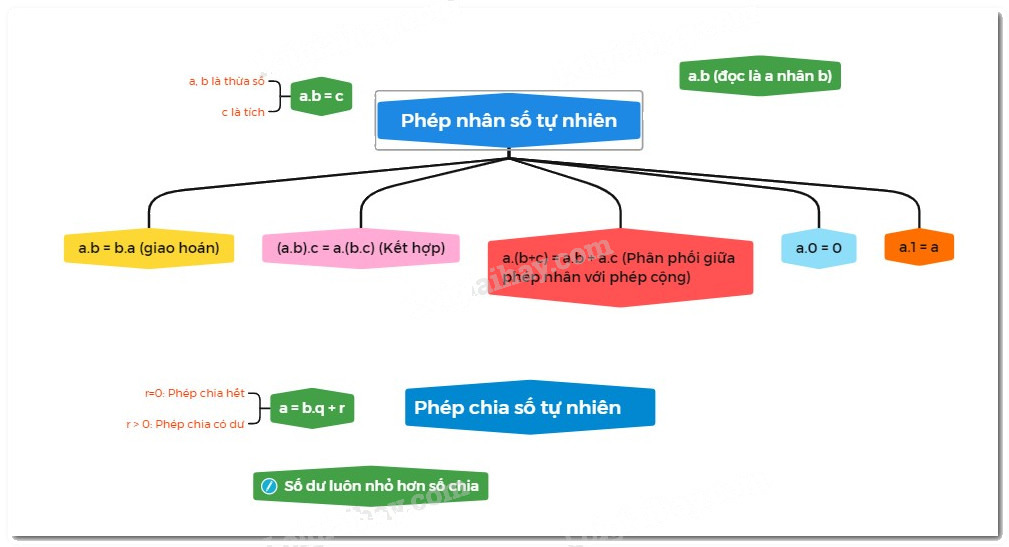
1. Phép nhân

$a.b = a + a + ... + a$ (Có b số hạng)

$a.b = d$

(thừa số) . (thừa số)  = (tích)

Tính chất của phép nhân:

Giao hoán:  $$a.b = b.a$$

Kết hợp:  $$\left( {a.b} \right).c = a.\left( {b.c} \right)$$

Phân phối của phép nhân đối với phép cộng:$a.\left( {b + c} \right) = a.b + a.c$

Ta hiểu tính chất phân phối ở đây là nếu a nhân với một tổng của b và c thì ta lấy a nhân với b và lấy a nhân với c rồi cộng lại với nhau. Chẳng hạn, $$2.\left( {3 + 5} \right) = 2.3 + 2.5$$ .

Lưu ý:

1) Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không viết dấu nhân giữa các thừa số. Chẳng hạn, $a \times b = a.b = ab$, $2 \times a = 2.a = 2a$.

2) Trong tính nhẩm ta thường sử dụng các kết quả:

2.5=10

4.25=100

8.125=1000

3) Tích $\left( {ab} \right)c$ hay $a\left( {bc} \right)$ gọi là tích cả ba số a, b, c và viết gọn là $abc$.

Ví dụ 1: Đặt tính nhân $254.45$

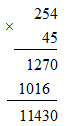
Ví dụ 2: Tính nhẩm 12.25

$12.25 = \left( {3.4} \right).25 = 3.\left( {4.25} \right) = 3.100 = 300$

2. Phép chia hết và phép chia có dư

Chia hai số tự nhiên

Cho hai số tự nhiên $a$  và $b,$  trong đó $b \ne 0$, ta luôn tìm được đúng hai số tự nhiên $q$  và $r$ duy nhất sao cho:

  $a = b.q + r$  trong đó  $0 \le r < b$

Nếu $r = 0$ thì ta có phép chia hết:

(số bị chia) : (số chia) = (thương)

Nếu $r \ne 0$ thì ta có phép chia có dư.

(số bị chia) = (số chia) . (thương) + (số dư)

Ví dụ 3:  Thực hiện các phép chia sau

a) 780:12

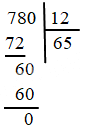
b) 445:13

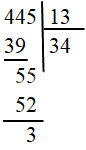
CÁC DẠNG TOÁN VỀ PHÉP NHÂN SÓ TỰ NHIÊN

I. Áp dụng các tính chất của phép nhân để tính nhanh

Phương pháp:

- Quan sát, phát hiện các đặc điểm của các thừa số.

- Từ đó, xét xem nên áp dụng tính chất nào (giao hoán, kết hợp, phân phối) để tính một cách nhanh chóng.

Đặc biệt: Viết một số dưới dạng một tích để tính nhanh

Phương pháp:

Bước 1: Căn cứ theo yêu cầu của đề bài, ta có thể viết một số tự nhiên đã cho dưới dạng một tích của hai hay nhiều thừa số.

Bước 2: Sử dụng tính chất giao hoán, kết hợp và phân phối để tính một cách hợp lí.

II. Tìm số chưa biết trong một đẳng thức (phép nhân)

Phương pháp:

+ Để tìm số chưa biết trong một phép tính, ta cần nắm vững quan hệ giữa các số trong phép tính. Chẳng hạn: thừa số bằng tích chia cho thừa số đã biết,…

+ Đặc biệt cần chú ý: với mọi $a$$\in$$N$ ta đều có $a.0 = 0;a.1 = a.$

+ Nếu tích hai thừa số bằng 0 thì có ít nhất một thừa số bằng 0.

Ví dụ: 

Tìm $x$, biết $x.5=65$.

Giải:

$x.5=65$

$x=65:5$

$x=13$

III. So sánh hai tích mà không tính cụ thể giá trị của chúng

Phương pháp:

Nhận xét, phát hiện và sử dụng các đặc điểm của các thừa số trong tổng hoặc tích. Từ đó dựa vào các tính chất phép nhân để rút ra kết luận.

Ví dụ:

So sánh hai tích sau mà không tính giá trị của chúng

$A = 2018.2018;B = 2017.2019$

Giải:

Ta có:

$\begin{array}{l}A = 2018.2018\\ = 2018.\left( {2017 + 1} \right)\\ = 2018.2017 + 2018.1\\ = 2018.2017 + 2018\\=2017.2018+2018\\B = 2017.2019\\ = 2017.\left( {2018 + 1} \right)\\ = 2017.2018 + 2017.1\\ = 2017.2018 + 2017\\ A= 2017.2018 + 2018=2017.2018+2017+1\\ = B + 1\\ \Rightarrow A = B+ 1\end{array}$

Vì $B+1 > B$ nên $A > B$.

IV. Tìm số tự nhiên có nhiều chữ số khi biết điều kiện xác định các chữ số trong số đó

Phương pháp:

Dựa vào điều kiện xác định các chữ số trong số tự nhiên cần tìm để tìm từng chữ số có mặt trong số tự nhiên đó.

Ví dụ:

Tìm một số tự nhiên có hai chữ số, biết rằng khi thêm 21 vào bên trái số đó thì được một số mới gấp 31 lần số cần tìm.
Giải:

Gọi số cần tìm là $\overline {ab}$, khi viết thêm số 21 vào bên trái số đó ta được số $\overline {21ab}$.

Vì $\overline {21ab}$ gấp 31 lần $\overline {ab}$ nên ta có:

$\begin{array}{l}\overline {ab}  \times 31 = \overline {21ab} \\\overline {ab}  \times 31 = 2100 + \overline {ab} \\\overline {ab}  \times 31 - \overline {ab}  \times 1 = 2100\\\overline {ab}  \times \left( {31 - 1} \right) = 2100\\\overline {ab}  \times 30 = 2100\\\overline {ab}  = 2100:30\\\overline {ab}  = 70\end{array}$