Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
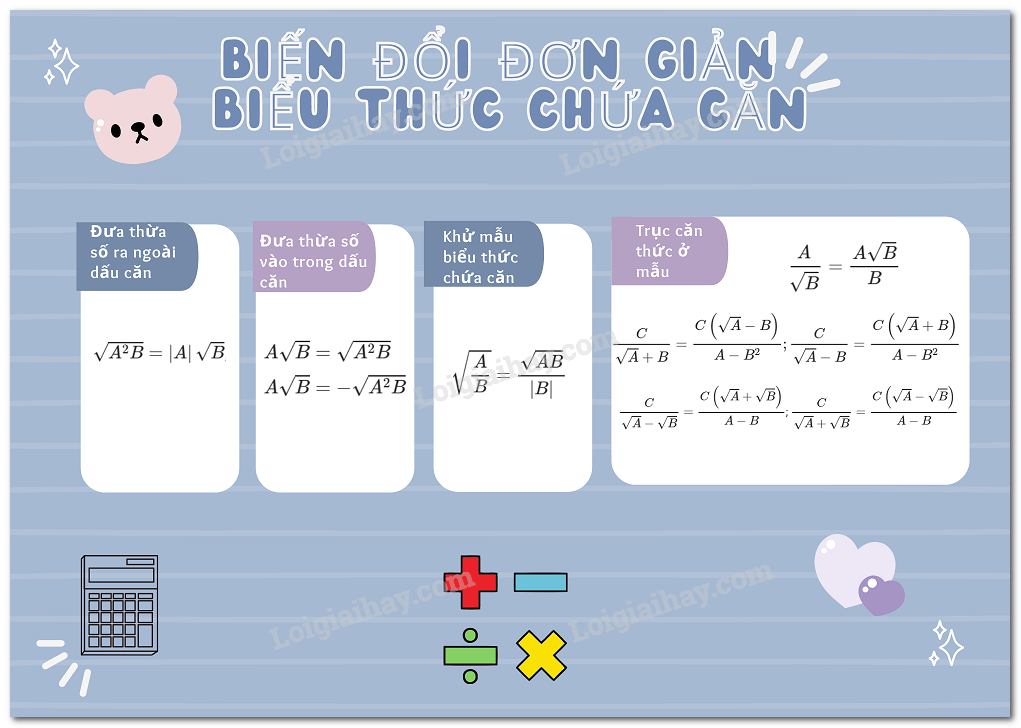
Lý thuyết về biến đổi đơn giản biểu thức chứa căn thức bậc hai( tiếp theo)
Trả lời câu hỏi 1 Bài 7 trang 28 SGK Toán 9 Tập 1 Trả lời câu hỏi 2 Bài 7 trang 29 Toán 9 Tập 1 Bài 48 trang 29 SGK Toán 9 tập 1 Bài 49 trang 29 SGK Toán 9 tập 1 Bài 50 trang 30 SGK Toán 9 tập 1 Bài 51 trang 30 SGK Toán 9 tập 1 Bài 52 trang 30 SGK Toán 9 tập 1 Bài 53 trang 30 SGK Toán 9 tập 1 Bài 54 trang 30 SGK Toán 9 tập 1 Bài 55 trang 30 SGK Toán 9 tập 1 Bài 56 trang 30 SGK Toán 9 tập 1 Bài 57 trang 30 SGK Toán 9 tập 1 Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 1 - Đại số 9 Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 1 - Đại số 9 Đề kiểm tra 15 phút - Đề số 3 - Bài 7 - Chương 1 - Đại số 9 Đề kiểm tra 15 phút - Đề số 4 - Bài 7 - Chương 1 - Đại số 9 Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 1 - Đại số 9Lý thuyết về biến đổi đơn giản biểu thức chứa căn thức bậc hai( tiếp theo)
Khử mẫu của biểu thức lấy căn Trục căn thức ở mẫu
1. Khử mẫu của biểu thức lấy căn
Với hai biểu thức A, B mà và , ta có:
Ví dụ: Với ta có:
2. Trục căn thức ở mẫu
Với hai biểu thức A, B mà ta có
Với các biểu thức A, B, C mà và , ta có
Với các biểu thức A, B, C mà , và , ta có:
Ví dụ: Trục căn thức ở mẫu của biểu thức với
Ta có:
CÁC DẠNG TOÁN VỀ BIẾN ĐỔI BIỂU THỨC CHỨA CĂN
Dạng 1: Đưa thừa số vào trong dấu căn, đưa thừa số ra ngoài dấu căn
Phương pháp:
Sử dụng các công thức
* Đưa thừa số ra ngoài dấu căn
Với hai biểu thức mà , ta có
* Đưa thừa số vào trong dấu căn
+) với và
+) với và
Dạng 2: So sánh hai căn bậc hai
Phương pháp:
Sử dụng công thức đưa thừa số ra ngoài dấu căn hoặc đưa thừa số vào trong dấu căn để so sánh hai căn bậc hai theo mối liên hệ
Dạng 3: Rút gọn biểu thức chứa căn thức bậc hai
Phương pháp:
Sử dụng công thức đưa thừa số ra ngoài dấu căn hoặc đưa thừa số vào trong dấu căn và hằng đẳng thức .
Sử dụng công thức trục căn thức ở mẫu
Dạng 4: Trục căn thức ở mẫu
Phương pháp:
Sử dụng các công thức
+) Với các biểu thức mà , ta có
+) Với các biểu thức mà , ta có
+) Với các biểu thức mà , ta có
+) Với các biểu thức mà ta có
;
Dạng 5: Giải phương trình
Phương pháp:
+) Tìm điều kiện
+) Sử dụng công thức đưa thừa số ra ngoài dấu căn hoặc đưa thừa số vào trong dấu căn để đưa phương trình về dạng cơ bản
+) So sánh điều kiện rồi kết luận nghiệm.

Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365