Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Lý thuyết Hàm số và đồ thị Toán 10
Tập xác định, tập giá trị của hàm số
Đồ thị của hàm số Sự biến thiên của hàm số Hàm số. Cách cho một hàm sốTập xác định, tập giá trị của hàm số
Tập xác định của hàm số y=f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa. Tập giá trị của hàm số y=f(x) là tập hợp tất cả các giá trị f(x) tương ứng với x thuộc tập xác định.
1. Lý thuyết
+ Định nghĩa:
Tập xác định của hàm số y=f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
Tập giá trị của hàm số y=f(x) là tập hợp tất cả các giá trị f(x) tương ứng với x thuộc tập xác định.
+ Kí hiệu:
Tập xác định thường kí hiệu là D. Ta nói: x∈D là điều kiện xác định của hàm số.
Tập giá trị thường kí hiệu là T.
+ Điều kiện xác định của một số biểu thức
√f(x) xác định khi f(x)≥0
1f(x) xác định khi f(x)≠0
1√f(x) xác định khi f(x)>0
2. Ví dụ minh họa
Dạng bảng
Tập xác định là tập hợp các giá trị x có trong bảng.
Tập giá trị là tập hợp các giá trị y có trong bảng.
Ví dụ: Dự báo thời tiết ngày 2/11/2022 tại Hà Nội
|
Giờ |
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
|
Nhiệt độ (oC) |
19 |
17 |
22 |
26 |
29 |
27 |
25 |
23 |
Tập xác định D={1;4;7;10;13;16;19;22}
Tập giá trị T={19;17;22;26;29;27;25;23}.
Dạng biểu đồ
Ví dụ: Dự báo thời tiết ngày 20/11/2021 tại Hà Nội
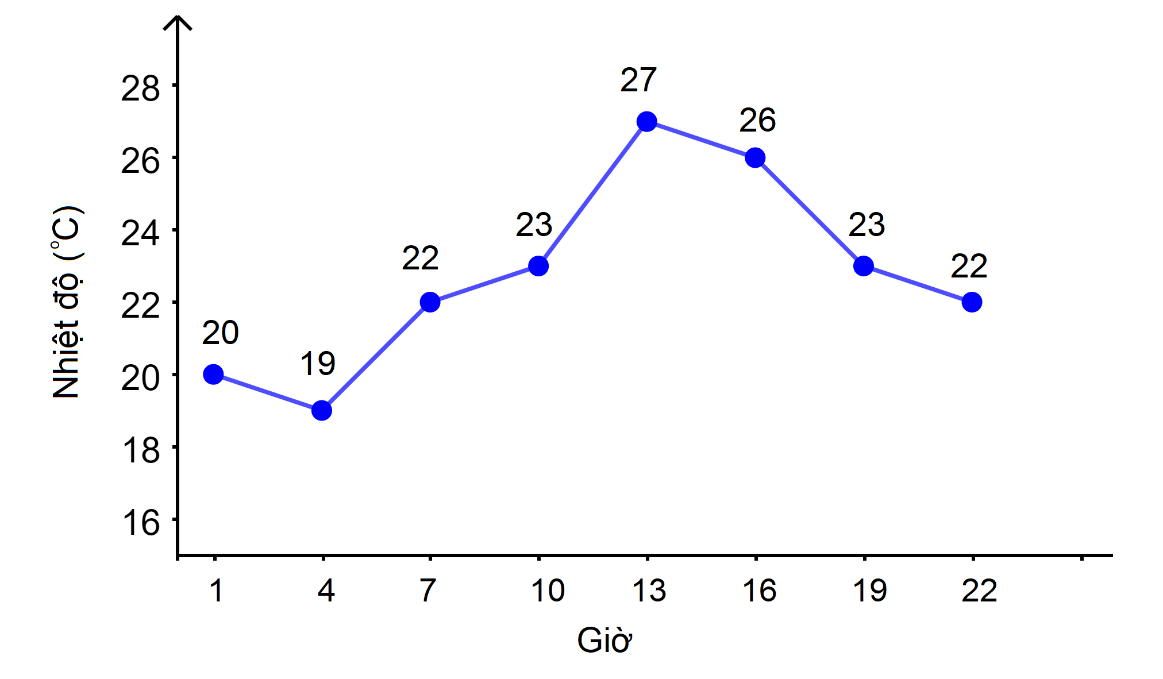
Tập xác định D={1;4;7;10;13;16;19;22}
Tập giá trị T={20;19;22;23;27;26}.
Dạng công thức
Ví dụ:
y=x2+3, biểu thức có nghĩa với mọi x∈R nên tập xác định là D=R
y=√x−1, biểu thức có nghĩa nếu x−1≥0 hay x≥1. Vậy tập xác định D=[1;+∞)
y={−3x+5x≤12x2x>2, ta xác đinh được y với x≤1 hoặc x>2, do đó tập xác định là D=(−∞;1]∪(2;+∞)
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365