Hình 2 biểu diễn các số hạng của dãy số \(\left( {{u_n}} \right),\) với \({u_n} = \frac{1}{n}\) trên hệ trục tọa độ.

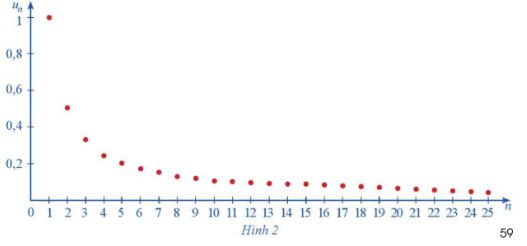
a) Nhận xét về sự thay đổi các giá trị \({u_n}\) khi n ngày càng lớn.

b) Hoàn thành bảng và trả lời câu hỏi sau:

Kể từ số hạng \({u_n}\) nào của dãy số thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,001? 0,0001?

Chứng minh rằng:

a) \(\lim 0 = 0;\)                           

b) \(\lim \frac{1}{{\sqrt n }} = 0.\) \(\)

Chứng minh rằng \(\lim \frac{{ - 4n + 1}}{n} =  - 4.\)

Chứng minh rằng \(\lim {\left( {\frac{e}{\pi }} \right)^n} = 0.\)