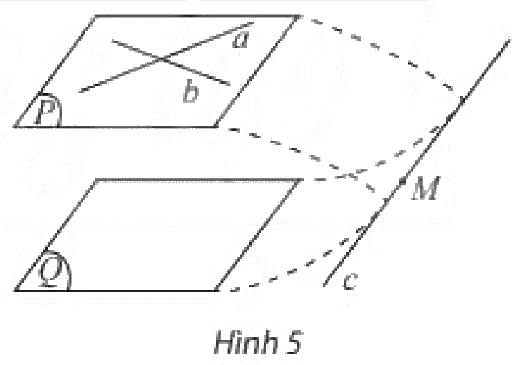
Cho mặt phẳng $\left( P \right)$ chứa hai đường thẳng $a,b$ cắt nhau và cùng song song với mặt phẳng $\left( Q \right)$. Giả sử $\left( P \right)$ và $\left( Q \right)$ có điểm chung $M$ thì $\left( P \right)$ cắt $\left( Q \right)$ theo giao tuyến $c$ (Hình 5).

a) Giải thích tại sao đường thẳng $c$ phải cắt ít nhất một trong hai đường thẳng $a,b$. Điều này có trái với giả thiết $a$ và $b$ cùng song song với $\left( Q \right)$ không?

b) Rút ra kết luận về số điểm chung và vị trí tương đối của $\left( P \right)$ và $\left( Q \right)$.

Cho tứ diện $ABCD$ có $E,F,H$lần lượt là trung điểm của $AB,AC,AD$. Chứng minh $\left( {EFH} \right)\parallel \left( {BCD} \right)$.