Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 25. Hai mặt phẳng vuông góc Toán 11 Kết nối tri thức
Giải mục 6 trang 51, 52 SGK Toán 11 tập 2 - Kết nối tri thức
Bài 7.16 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức Bài 7.17 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức Bài 7.18 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức Bài 7.19 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức Bài 7.20 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức Bài 7.21 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 5 trang 49, 50 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 4 trang 47, 48 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 3 trang 46, 47 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 2 trang 45, 46 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 1 trang 44, 45 SGK Toán 11 tập 2 - Kết nối tri thức Lý thuyết Hai mặt phẳng vuông góc - Toán 11 Kết nối tri thứcGiải mục 6 trang 51, 52 SGK Toán 11 tập 2 - Kết nối tri thức
Tháp lớn tại Bảo tàng Louvre ở Paris (H.7.66)
HĐ11
Tháp lớn tại Bảo tàng Louvre ở Paris (H.7.66) (với kết cấu kính và kim loại) có dạng hình chóp với đây là hình vuông có cạnh bằng 34 m, các cạnh bên bằng nhau và có độ dài xấp xỉ 32,3 m (theo Wikipedia.org).
Giải thích vì sao hình chiếu của đỉnh trên đây là tâm của đáy tháp.

HĐ12
Cho hình chóp S.A1A2...An. Gọi O là hình chiếu của S trên mặt phẳng (A1A2...An).
a) Trong trường hợp hình chóp đã cho là đều, vị trí của điểm O có gì đặc biệt đối với đa giác đều A1A2...An?
b) Nếu đa giác A1A2...An là đều và O là tâm của đa giác đó thì hình chóp đã cho có gì đặc biệt?
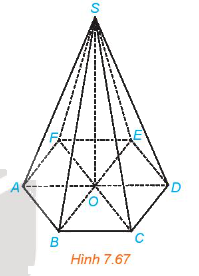
LT5
Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng Tính số đo của góc nhị diện [S, BC, A].
HĐ13
Cho hình chóp đều S.A1A2...An. Một mặt phẳng không đi qua S và song song với mặt phẳng đáy, cắt các cạnh SA1, SA2,.... SAn, tương ứng tai B1, B2,..., Bn
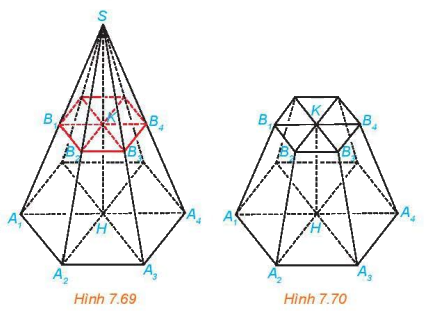
a) Giải thích vì sao S. B1B2...Bn là một hình chóp đều.
b) Gọi H là tâm của đa giác A1A2...An. Chứng minh rằng đường thẳng SH đi qua tâm K của đa giác đều B1B2...Bn, và HK vuông góc với các mặt phẳng (A1A2...An), (B1B2...Bn)
CH2
Hình chóp cụt đều có các cạnh bên bằng nhau hay không?
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365