Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 31. Định nghĩa và ý nghĩa của đạo hàm Toán 11 Kết nối tri thức
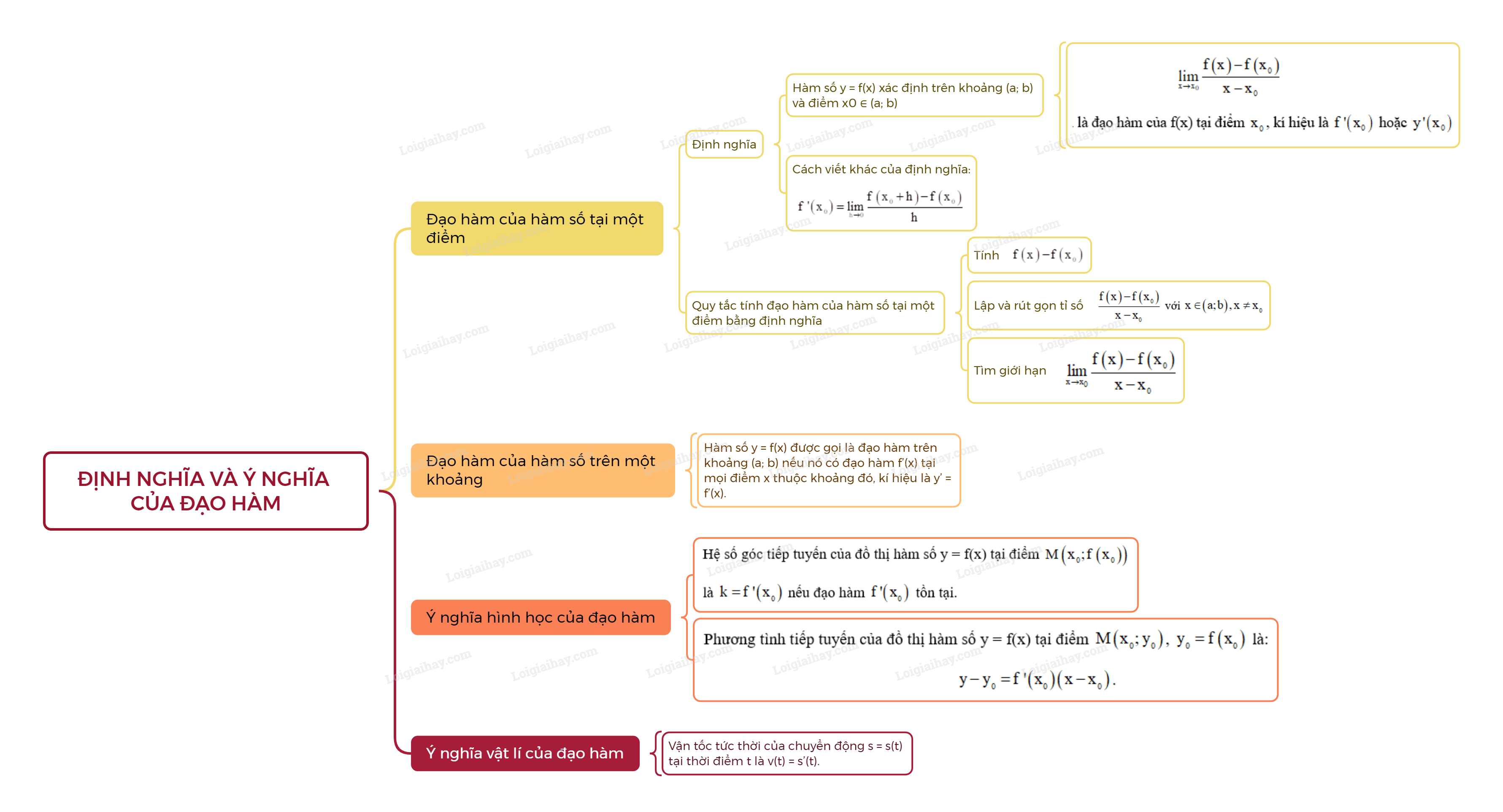
Lý thuyết Định nghĩa và ý nghĩa của đạo hàm - Toán 11 Kết nối tri thức
Giải mục 1 trang 81, 82 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 2 trang 83 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 3 trang 83, 84 SGK Toán 11 tập 2 - Kết nối tri thức Giải mục 4 trang 84, 85 SGK Toán 11 tập 2 - Kết nối tri thức Bài 9.1 trang 86 SGK Toán 11 tập 2 - Kết nối tri thức Bài 9.2 trang 86 SGK Toán 11 tập 2 - Kết nối tri thức Bài 9.3 trang 86 SGK Toán 11 tập 2 - Kết nối tri thức Bài 9.4 trang 86 SGK Toán 11 tập 2 - Kết nối tri thức Bài 9.5 trang 86 SGK Toán 11 tập 2 - Kết nối tri thứcLý thuyết Định nghĩa và ý nghĩa của đạo hàm - Toán 11 Kết nối tri thức
1. Đạo hàm của hàm số tại một điểm
1. Đạo hàm của hàm số tại một điểm
- Định nghĩa: Cho hàm số y = f(x) xác định trên khoảng (a;b) và điểm x0∈(a;b). Nếu tồn tại giới hạn (hữu hạn)
limx→x0f(x)−f(x0)x−x0
thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm x0, kí hiệu là f′(x0) hoặc y′(x0).
- Cách viết khác của định nghĩa:
f′(x0)=limh→0f(x0+h)−f(x0)h.
- Quy tắc tính đọa hàm của hàm số tại một điểm bằng định nghĩa:
Bước 1: Tính f(x)−f(x0).
Bước 2: Lập và rút gọn tỉ số f(x)−f(x0)x−x0 với x∈(a;b),x≠x0.
Bước 3: Tìm giới hạn limx→x0f(x)−f(x0)x−x0.
2. Đạo hàm của hàm số trên một khoảng
Hàm số y = f(x) được gọi là đạo hàm trên khoảng (a; b) nếu nó có đạo hàm f’(x) tại mọi điểm x thuộc khoảng đó, kí hiệu là y’ = f’(x).
3. Ý nghĩa hình học của đạo hàm
- Hệ số góc tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0;f(x0)) là k=f′(x0) nếu đạo hàm f′(x0) tồn tại.
- Phương tình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0;y0), y0=f(x0) là:
y−y0=f′(x0)(x−x0).
4. Ý nghĩa vật lí của đạo hàm
Vận tốc tức thời của chuyển động s = s(t) tại thời điểm t là v(t) = s’(t).
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365