Trả lời câu hỏi Hoạt động 2 trang 16 SGK Toán 12 Cánh diều

Cho hàm số $f\left( x \right) = x + \frac{1}{{x - 1}}$ với $x > 1$.

a) Tính $\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right)$.

b) Lập bảng biến thiên của hàm số $f\left( x \right)$ trên khoảng $\left( {1; + \infty } \right)$.

c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $f\left( x \right)$ trên khoảng $\left( {1; + \infty } \right)$.

Trả lời câu hỏi Luyện tập 2 trang 16 SGK Toán 12 Cánh diều

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $y = \frac{{2x - 5}}{{x - 1}}$ trên nửa khoảng $(1;3]$.

Trả lời câu hỏi Hoạt động 3 trang 17 SGK Toán 12 Cánh diều

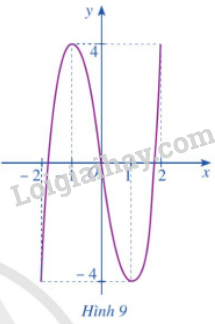
Cho hàm số $y = f\left( x \right) = 2{x^3} - 6x,x \in \left[ { - 2;2} \right]$ có đồ thị là đường cong ở Hình 9.

a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị $M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right);m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right)$ bằng bao nhiêu.

b) Giải phương trình $f'\left( x \right) = 0$ với $x \in \left( { - 2;2} \right)$

c) Tính các giá trị của hàm số $f\left( x \right)$ tại hai đầu mút $- 2;2$ và tại các điểm $x \in \left( { - 2;2} \right)$ mà ở đó $f'\left( x \right) = 0$

d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c

Trả lời câu hỏi Luyện tập 3 trang 18 SGK Toán 12 Cánh diều

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right) = \sin 2x - 2x$ trên đoạn $\left[ {\frac{\pi }{2};\frac{{3\pi }}{2}} \right]$.