Trả lời câu hỏi Hoạt động 2 trang 58 SGK Toán 12 Cánh diều

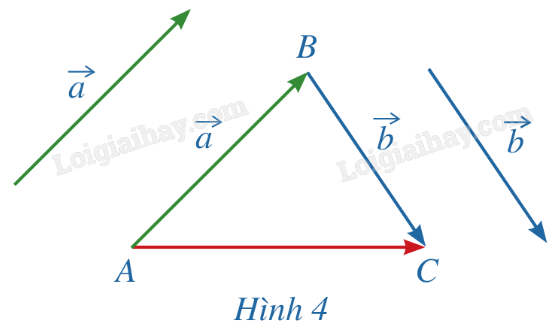
Trong không gian, cho 2 vecto $\vec a$ và $\vec b$. Lấy một điểm A tùy ý.

a) Vẽ $\overrightarrow {AB}  = \vec a$, $\overrightarrow {BC}= \vec b$.

b) Tổng của 2 vecto $\vec a$ và $\vec b$ bằng vec tơ nào trong Hình 4?

Trả lời câu hỏi Luyện tập 2 trang 58 SGK Toán 12 Cánh diều

Cho tứ diện ABCD. Chứng minh rằng $\overrightarrow {AC}  + \overrightarrow {DB}  = \overrightarrow {AB}  + \overrightarrow {DC}$.

Trả lời câu hỏi Hoạt động 3 trang 59 SGK Toán 12 Cánh diều

Cho hình hộp ABCD.A’B’C’D’. Tìm liên hệ giữa $\overrightarrow {AB}  + \overrightarrow {AD}$ và $\overrightarrow {AC}$; $\overrightarrow {AC}  + \overrightarrow {AA'}$ và $\overrightarrow {AC'}$.

Trả lời câu hỏi Luyện tập 3 trang 59 SGK Toán 12 Cánh diều

Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng: $\overrightarrow {B'B}  + \overrightarrow {AD}  + \overrightarrow {CD}  = \overrightarrow {B'D}$.

Trả lời câu hỏi Hoạt động 4 trang 59 SGK Toán 12 Cánh diều

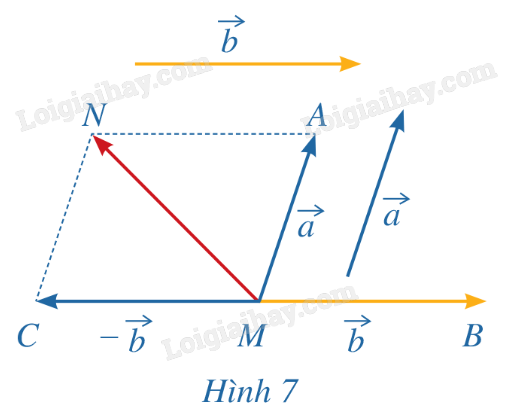
Trong không gian, cho hai vecto $\vec a$, $\vec b$. Lấy một điểm M tùy ý.

a) Vẽ $\overrightarrow {MA}  = \vec a$, $\overrightarrow {MB}  = \vec b$, $\overrightarrow {MC}  = \overrightarrow { - b}$.

b) Tổng của hai vecto $\vec a$ và $\overrightarrow { - b}$ bằng vecto nào trong Hình 7.

Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cánh diều

Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng: $\overrightarrow {BB'}  - \overrightarrow {C'B'}  - \overrightarrow {D'C'}  = \overrightarrow {BD'}$.

Trả lời câu hỏi Hoạt động 5 trang 60 SGK Toán 12 Cánh diều

Nêu định nghĩa tích của một số thực $k \ne 0$ với vecto $\vec a \ne \vec 0$ trong mặt phẳng.

Trả lời câu hỏi Luyện tập 5 trang 60 SGK Toán 12 Cánh diều

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điển của các cạnh AD và BC, I là trung điểm của MN. Chứng minh rằng:

a) $\overrightarrow {MN}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {DC} } \right)$.

b) $\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  + \overrightarrow {ID}  = \overrightarrow 0$.

Trả lời câu hỏi Hoạt động 6 trang 61 SGK Toán 12 Cánh diều

Trong không gian, cho hai vecto $\vec a$, $\vec b$ khác $\vec 0$. Lấy một điểm O tùy ý.

a) Vẽ hai vecto $\overrightarrow {OA}  = \vec a$, $\overrightarrow {OB}  = \vec b$.

b) Khi đó, hai vecto $\overrightarrow {OA}$, $\overrightarrow {OB}$ có giá nằm trong cùng mặt phẳng (P) (Hình 10). Nêu định nghĩa góc giữa hai vecto $\overrightarrow {OA}$, $\overrightarrow {OB}$ trong mặt phẳng (P).

Trả lời câu hỏi Luyện tập 6 trang 61 SGK Toán 12 Cánh diều

Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, AC. Hãy tính góc giữa hai vecto $\overrightarrow {MN}$, $\overrightarrow {BD}$.

Trả lời câu hỏi Hoạt động 7 trang 61 SGK Toán 12 Cánh diều

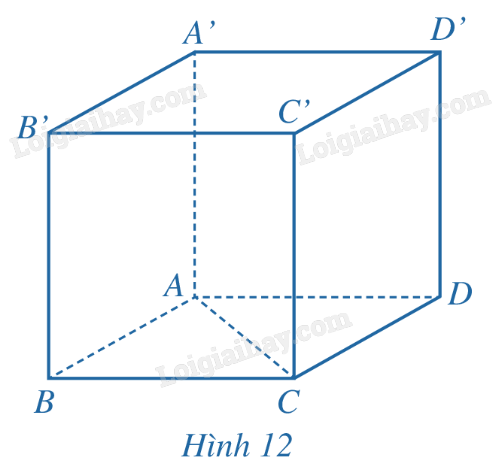
Trong không gian, cho hình lập phương ABCD.A’B’C’D’ có độ dài bằng 3cm (Hình 12).

a) Tính góc giữa hai vecto $\overrightarrow {AC}$, $\overrightarrow {A'D'}$.

b) Tính $\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {A'D'} } \right|.cos(\overrightarrow {AC} ,\overrightarrow {A'D'}$).

Trả lời câu hỏi Luyện tập 7 trang 62 SGK Toán 12 Cánh diều

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính $\overrightarrow {A'B} .\overrightarrow {D'C'}$; $\overrightarrow {D'A} .\overrightarrow {BC}$.