Câu 1:

a) Tính giá trị của biểu thức $A = \sqrt {80}  + \sqrt {45}$.

b) Rút gọn biểu thức $B = \left( {\frac{1}{{\sqrt x  - 1}} + \frac{3}{{\sqrt x  + 1}}} \right):\frac{2}{{\sqrt x  + 1}}$ với $x > 0$ và $x \ne 1$.

Câu 2:

a) Tìm hệ số a để đồ thị hàm số $y = a{x^2}$đi qua điểm M(-1;2). Vẽ đồ thị của hàm số $y = a{x^2}$ với giá trị $a$ vừa tìm được.

b) Giải hệ phương trình $\left\{ \begin{array}{l}x - 2y = 4\\2x + y = 3\end{array} \right.$

Câu 3:

Cho phương trình bậc hai ${x^2} - 2x + m - 2 = 0$ (1), với $m$ là tham số.

a) Xác định các hệ số a, b, c của phương trình (1).

b) Giải phương trình (1)  khi $m =  - 1$.

c) Tìm giá trị của $m$ để phương trình (1) có hai nghiệm ${x_1},{x_2}$ thỏa mãn $3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11$.

Câu 4:

Trên đường tròn tâm O, đường kính AB = 2R, lấy hai điểm C, D sao cho CD vuông góc với AB tại H (H thuộc đoạn OA, khác O và A). Gọi M là điểm trên đoạn CD (M khác C và D, CM > DM), E là giao điểm của AM với đường tròn (O), N là giao điểm của hai đường thẳng BE và CD.

a) Chứng minh tứ giác MEBH nội tiếp

b) Chứng minh NC. ND = NB. NE

c) Khi AC = R, xác định vị trí của điểm M để 2AM + AE đạt giá trị nhỏ nhất

-----HẾT-----

Câu 1 (TH):

Phương pháp:

a) Biến đổi $\sqrt {{A^2}}  = \left| A \right|$ và $\sqrt {A.B}  = \sqrt A .\sqrt B$

b) Tìm mẫu số chung, quy đồng và rút gọn biểu thức

Cách giải:

a) Tính giá trị của biểu thức $A = \sqrt {80}  + \sqrt {45}$.

Ta có:

$\begin{array}{l}A = \sqrt {80}  + \sqrt {45} \\A = \sqrt {16.5}  + \sqrt {9.5} \\A = \sqrt {{4^2}.5}  + \sqrt {{3^2}.5} \\A = 4\sqrt 5  + 3\sqrt 5 \\A = 7\sqrt 5 \end{array}$

Vậy $A = 7\sqrt 5$.

b) Rút gọn biểu thức $B = \left( {\frac{1}{{\sqrt x  - 1}} + \frac{3}{{\sqrt x  + 1}}} \right):\frac{2}{{\sqrt x  + 1}}$ với $x > 0$ và $x \ne 1$.

Với $x > 0$ và $x \ne 1$ ta có:

$\begin{array}{l}B = \left( {\frac{1}{{\sqrt x  - 1}} + \frac{3}{{\sqrt x  + 1}}} \right):\frac{2}{{\sqrt x  + 1}}\\B = \frac{{\sqrt x  + 1 + 3\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}:\frac{2}{{\sqrt x  + 1}}\\B = \frac{{\sqrt x  + 1 + 3\sqrt x  - 3}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}.\frac{{\sqrt x  + 1}}{2}\\B = \frac{{4\sqrt x  - 2}}{{\sqrt x  - 1}}.\frac{1}{2}\\B = \frac{{2\sqrt x  - 1}}{{\sqrt x  - 1}}\end{array}$

Vậy $B = \frac{{2\sqrt x  - 1}}{{\sqrt x  - 1}}.$

Câu 2 (TH):

Phương pháp:

a) Thay tọa độ M vào hàm số tìm a, lập bảng vẽ đồ thị hàm số và nhận xét

b) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số

Cách giải:

a) Tìm hệ số a để đồ thị hàm số $y = a{x^2}$đi qua điểm M(-1;2). Vẽ đồ thị của hàm số $y = a{x^2}$ với giá trị $a$ vừa tìm được.

Đồ thị hàm số $y = a{x^2}$đi qua điểm $M\left( { - 1;2} \right)$ khi và chỉ khi: $a.{\left( { - 1} \right)^2} = 2 \Leftrightarrow a = 2$

Vậy $a = 2$.

* Vẽ đồ thị hàm số $y = 2{x^2}$

Ta có bảng giá trị sau:

=> Đồ thị hàm số là đường cong parabol đi qua các điểm $O\,\left( {0;0} \right);A\left( { - 1;2} \right);\,\,B\left( {1;2} \right);\,C\left( { - 2;8} \right);\,D\left( {2;8} \right)$.

Hệ số a = 2 > 0 nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.

Ta vẽ được đồ thị hàm số $y = 2{x^2}$ như sau:

b) Giải hệ phương trình $\left\{ \begin{array}{l}x - 2y = 4\\2x + y = 3\end{array} \right.$

Ta có: $\left\{ \begin{array}{l}x - 2y = 4\\2x + y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2y = 4\\4x + 2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\y = 3 - 2x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y =  - 1\end{array} \right.$

Vậy hệ phương trình có nghiệm duy nhất là: $\left( {x;y} \right) = \left( {2; - 1} \right)$.

Câu 3 (TH):

Phương pháp:

a) Hệ số a, b, c của phương trình là các hệ số của số hạng ${x^2},x$và hệ số tự do

b) Thay m = -1 vào phương trình, giải phương trình bằng cách nhẩm nghiệm

c) Tính $\Delta '$. Cho $\Delta ' > 0$ tìm m, áp dụng Viet thay vào $3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11$

Cách giải:

a) Xác định các hệ số a, b, c của phương trình (1).

Hệ số $a = 1;\,\,b =  - 2;\,\,c = m - 2.$

b) Giải phương trình (1)  khi $m =  - 1$.

Khi $m =  - 1$ phương trình (1)  $\Leftrightarrow {x^2} - 2x - 3 = 0$.

Ta có $a - b + c = 1 - \left( { - 2} \right) + \left( { - 3} \right) = 0$ nên phương trình có hai nghiệm phân biệt $\left[ \begin{array}{l}{x_1} =  - 1\\{x_2} =  - \frac{c}{a} = 3\end{array} \right.$.

Vậy khi m = -1 thì tập nghiệm của phương trình là $S = \left\{ { - 1;3} \right\}$.

c) Tìm giá trị của $m$ để phương trình (1) có hai nghiệm ${x_1},{x_2}$ thỏa mãn $3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11$.

Phương trình (1) có  $\Delta ' = {\left( { - 1} \right)^2} - 1\left( {m - 2} \right) =  - m + 3$.

Để phương trình có hai nghiệm thì $\Delta ' \ge 0 \Leftrightarrow  - m + 3 \ge 0 \Leftrightarrow m \le 3$

Áp dụng định lí Vi – ét ta có:$\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}.{x_2} = m - 2}\end{array}} \right.$

Theo bài ra ta có: $3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11$

$\Leftrightarrow 3\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}.{x_2}} \right] + x_1^2x_2^2 = 11$ (2)

Thay $\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}.{x_2} = m - 2}\end{array}} \right.$ vào (2) ta có:

$\begin{array}{l} \Leftrightarrow 3\left[ {{2^2} - 2\left( {m - 2} \right)} \right] + {\left( {m - 2} \right)^2} = 11\\ \Leftrightarrow 3\left( {8 - 2m} \right) + {m^2} - 4m + 4 = 11\\ \Leftrightarrow {m^2} - 10m + 17 = 0\,\,\left( * \right)\end{array}$

Ta có: ${\Delta _m}' = {5^2} - 17 = 8 > 0$ nên phương trình (*) có hai nghiệm phân biệt $\left[ \begin{array}{l}m = 5 + 2\sqrt 2 \,\,\,\left( {ktm} \right)\\m = 5 - 2\sqrt 2 \,\,\,\left( {tm} \right)\end{array} \right.$

Vậy với $m = 5 - 2\sqrt 2 \,$ phương trình (1) có hai nghiệm ${x_1},{x_2}$ thỏa mãn $3\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2 = 11$.

Câu 4 (VD):

Phương pháp:

a) Tổng hai góc đối bằng ${180^0}$

b) Chứng minh $\Delta NCE\backsim \Delta NBD\left( g.g \right)$

c) Gọi $HM = x\,\,\left( {0 < x < R} \right)$. Tính AE, AM theo x và áp dụng bất đẳng thức Cô-si

Cách giải:

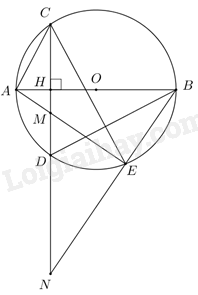
a) Chứng minh tứ giác MEBH nội tiếp

Ta có $\angle AEB = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

         $\angle MHB = {90^0}$ (do $CD \bot AB$ tại H) (gt)

$\Rightarrow \angle MEB + \angle MHB = {90^0} + {90^0} = {180^0}$.

Mà 2 góc này ở vị trí đối diện nên tứ giác MEBH nội tiếp (dhnb)

b) Chứng minh NC. ND = NB. NE

Xét $\Delta NCE$ và $\Delta NBD$ có:

$\angle BNC$ chung

$\angle NCE = \angle NBD$ (góc nội tiếp cùng chắn cung DE)

$\Rightarrow \Delta NCE\backsim \Delta NBD\left( g.g \right)$

$\Rightarrow \frac{{NC}}{{NB}} = \frac{{NE}}{{ND}} \Leftrightarrow NC.ND = NE.NB$ (đpcm)

c) Khi AC = R, xác định vị trí của điểm M để 2AM + AE đạt giá trị nhỏ nhất

Xét tam giác OAC có OA = OC = AC = R => Tam giác OAC đều.

$\Rightarrow$ Đường cao CH đồng thời là đường trung tuyến $\Rightarrow H$ là trung điểm của OA $\Rightarrow AH = \frac{1}{2}OA = \frac{R}{2}$.

Đặt $HM = x\,\,\left( {0 < x < R} \right)$.

Áp dụng định lí Pytago trong tam giác vuông AHM ta có: $AM = \sqrt {\frac{{{R^2}}}{4} + {x^2}}  \Rightarrow 2AM = \sqrt {{R^2} + 4{x^2}}$.

Xét tam giác AHM và tam giác AEB có:

$\begin{array}{l}\angle BAE\,\,chung\\\angle AHM = \angle AEB = {90^0}\,\,\left( {cmt} \right)\end{array}$

$\Rightarrow \Delta AHM\backsim \Delta AEB\,\,\left( g.g \right)$

$\Rightarrow \frac{{HM}}{{BE}} = \frac{{AH}}{{AE}} = \frac{{AM}}{{AB}}$ (các cặp cạnh tương ứng tỉ lệ).

$\Rightarrow AE = \frac{{AH.AB}}{{AM}} = \frac{{\frac{R}{2}.2R}}{{\sqrt {\frac{{{R^2}}}{4} + {x^2}} }} = \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}$

$\Rightarrow 2AM + AE = \sqrt {{R^2} + 4{x^2}}  + \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}$

Áp dụng BĐT Cô-si ta có:

$\sqrt {{R^2} + 4{x^2}}  + \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }} \ge 2\sqrt {\sqrt {{R^2} + 4{x^2}} .\frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}}  = 2\sqrt 2 R$

Dấu “=” xảy ra

$\begin{array}{l} \Leftrightarrow \sqrt {{R^2} + 4{x^2}}  = \frac{{2{R^2}}}{{\sqrt {{R^2} + 4{x^2}} }}\\ \Leftrightarrow {R^2} + 4{x^2} = 2{R^2} \Leftrightarrow {x^2} = \frac{{{R^2}}}{4} \Leftrightarrow x = \frac{R}{2}\,\,\left( {tm} \right)\end{array}$

$\Rightarrow HM = \frac{R}{2} \Rightarrow M$ là trung điểm của HD.

Vậy để 2AM + AE đạt giá trị nhỏ nhất thì M là trung điểm của HD.