Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi vào 10 môn Toán Bạc Liêu năm 2021
Câu 1 (4,0 điểm): a) Rút gọn biểu thức
Đề bài
Câu 1 (4,0 điểm):
a) Rút gọn biểu thức A=√28+√63−2√7A=√28+√63−2√7
b) Chứng minh rằng: x√y+y√x√xy:1√x−√y=x−yx√y+y√x√xy:1√x−√y=x−y với x>0,y>0x>0,y>0 và x≠yx≠y.
Câu 2 (4,0 điểm):
a) Giải hệ phương trình: {x−2y=52x−y=7.{x−2y=52x−y=7.
b) Cho hàm số y=−14x2y=−14x2 có đồ thị (P)(P) và đường thẳng d:y=12x−2.d:y=12x−2. Vẽ đồ thị (P)(P) và tìm tọa độ giao điểm của (P)(P) với đường thẳng dd bằng phép tính.
Câu 3 (6,0 điểm):
Cho phương trình x2−(m+2)x+m+1=0(1)x2−(m+2)x+m+1=0(1) (mm là tham số).
a) Giải phương trình khi m=−3m=−3.
b) Chứng minh phương trình (1)(1) luôn có nghiệm với mọi số thực m.m.
c) Tìm mm để phương trình (1) có hai nghiệm phân biệt x1,x2x1,x2 là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài đường cao kẻ từ đỉnh góc vuông xuống cạnh huyền là h=2√5h=2√5.
Câu 4 (6,0 điểm):
Cho đường tròn (O;R)(O;R) và đường thẳng dd không đi qua OO cắt đường tròn (O)(O) tại hai điểm A,BA,B. Trên tia đối của tia BABA, lấy một điểm MM, qua MM kẻ hai tiếp tuyến MCMC và MDMD với đường tròn (O)(O) (C,DC,D là các tiếp điểm). Gọi HH là trung điểm của ABAB.
a) Chứng minh rằng tứ giác OMCHOMCH nội tiếp được trong một đường tròn.
b) OMOM cắt đường tròn (O)(O) tại II và cắt CDCD tại KK. Chứng minh OK.OM=R2OK.OM=R2.
c) Đường thẳng qua OO vuông góc với OMOM cắt các tia MCMC và MDMD lần lượt tại PP và QQ. Tính độ dài OMOM theo RR sao cho diện tích tam giác MPQMPQ nhỏ nhất.
Lời giải
Câu 1 (TH)
Phương pháp:
a) Vận dụng hằng đẳng thức √A2=|A|={AkhiA≥0−AkhiA<0√A2=|A|={AkhiA≥0−AkhiA<0
Thực hiện các phép toán với các căn bậc hai.
b) Thực hiện phép chia với các phân thức đại số
Tìm các hạng tử chung của tử thức và mẫu thức sau đó rút gọn biểu thức để chứng minh.
Cách giải:
a) Ta có
A=√28+√63−2√7A=√22.7+√32.7−2√7A=2√7+3√7−2√7A=3√7A=√28+√63−2√7A=√22.7+√32.7−2√7A=2√7+3√7−2√7A=3√7
Vậy A=3√7A=3√7.
b) Với x>0,y>0x>0,y>0 và x≠yx≠y ta có:
VT=x√y+y√x√xy:1√x−√y=√xy(√x+√y)√xy.(√x−√y)=(√x+√y).(√x−√y)=x−y=VPVT=x√y+y√x√xy:1√x−√y=√xy(√x+√y)√xy.(√x−√y)=(√x+√y).(√x−√y)=x−y=VP
Vậy ta có điều phải chứng minh.
Câu 2 (VD)
Phương pháp:
a) Vận dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình.
b) + Lập bảng giá trị tương ứng của xx và yy của đồ thị (P)(P)
+ Xét phương trình hoành độ giao điểm của dd và (P)(P)
Áp dụng công thức nghiệm của phương trình bậc hai một ẩn, tìm được nghiệm của phương trình
Với mỗi nghiệm ta tìm được các giao điểm của dd và (P)(P), từ đó kết luận.
Cách giải:
a) {x−2y=52x−y=7⇔{x−2y=54x−2y=14⇔{3x=9y=2x−7{x−2y=52x−y=7⇔{x−2y=54x−2y=14⇔{3x=9y=2x−7⇔{x=3y=2.3−7⇔{x=3y=−1⇔{x=3y=2.3−7⇔{x=3y=−1
Vậy hệ phương trình có nghiệm duy nhất (x;y)=(3;−1).(x;y)=(3;−1).
b) Vẽ đồ thị hàm số y=−14x2.y=−14x2.
Ta có bảng giá trị:
|
xx |
−4−4 |
−2−2 |
00 |
22 |
44 |
|
y=−14x2y=−14x2 |
−4−4 |
−1−1 |
00 |
−1−1 |
−4−4 |
Vậy đồ thị hàm số (P):y=−14x2(P):y=−14x2 là đường cong đi qua các điểm (−4;−4),(−2;−1),(0;0),(2;−1),(4;−4).(−4;−4),(−2;−1),(0;0),(2;−1),(4;−4).
Đồ thị hàm số:
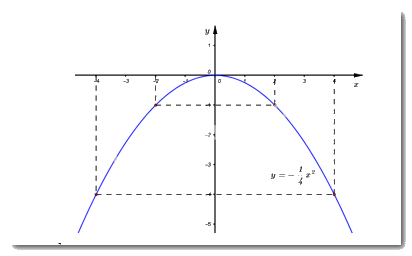
Phương trình hoành độ giao điểm của dd và (P)(P) là:
−14x2=12x−2⇔−x2=2x−8⇔x2+2x−8=0−14x2=12x−2⇔−x2=2x−8⇔x2+2x−8=0
Phương trình có: Δ′=(−1)2+8=9>0Δ′=(−1)2+8=9>0
⇒⇒ Phương trình có hai nghiệm phân biệt: x1=−1+√9=2x1=−1+√9=2 và x2=−1−√9=−4x2=−1−√9=−4
Với x=2x=2 ⇒y=−14.22=−1.⇒y=−14.22=−1.
Với x=−4x=−4⇒y=−14.(−4)2=−4.⇒y=−14.(−4)2=−4.
Vậy đường thẳng dd cắt (P)(P) tại hai điểm phân biệt (2;−1)(2;−1) và (−4;−4).(−4;−4).
Câu 3 (VD):
Phương pháp:
a) Thay m=−3m=−3 vào phương trình, ta có được phương trình bậc hai một ẩn
Áp dụng công thức nhẩm nghiệm nhanh: phương trình ax2+bx+c=0(a≠0)ax2+bx+c=0(a≠0) nếu có a+b+c=0a+b+c=0 thì phương trình có hai nghiệm phân biệt x1=1;x2=cax1=1;x2=ca
b) Phương trình luôn có nghiệm với mọi số thực mm khi Δ≥0,∀mΔ≥0,∀m
c) + Phương trình có hai nghiệm phân biệt ⇔Δ>0⇔Δ>0
+ Áp dụng định lí Vi – ét, tính được x1+x2;x1.x2x1+x2;x1.x2 theo tham số mm
+ Do hai nghiệm phân biệt x1,x2x1,x2 là độ dài hai cạnh góc vuông nên ta có: x1,x2>0x1,x2>0 suya ra điều kiện của mm
+ Áp dụng hệ thức lượng trong tam giác vuông, ta có hệ thức 1x21+1x22=1(2√5)21x21+1x22=1(2√5)2. Biến đổi hệ thức, xuất hiện x1+x2;x1.x2x1+x2;x1.x2 sau đó thay tham số mm thực hiện tính toán.
Cách giải:
a) Khi m=−3m=−3 phương trình (1) trở thành x2+x−2=0x2+x−2=0.
Vì a+b+c=1+1+(−2)=0a+b+c=1+1+(−2)=0 nên phương trình có 2 nghiệm phân biệt [x=1x=ca=−2[x=1x=ca=−2
Vậy khi m=−3m=−3 thì phương trình có tập nghiệm S={1;−2}S={1;−2},.
b) Ta có: hệ số của x2x2 là 1≠01≠0 nên phương trình (1)(1) là phương trình bậc hai một ẩn.
Lại có: Δ=(m+2)2−4(m+1)=m2+4m+4−4m−4=m2≥0∀mΔ=(m+2)2−4(m+1)=m2+4m+4−4m−4=m2≥0∀m.
Do đó phương trình (1)(1) luôn có nghiệm với mọi số thực m.m.
c) Phương trình (1) có: Δ=(m+2)2−4(m+1)=m2+4m+4−4m−4=m2Δ=(m+2)2−4(m+1)=m2+4m+4−4m−4=m2.
Để phương trình (1) có 2 nghiệm phân biệt x1,x2x1,x2 thì Δ>0⇔m2>0⇔m≠0Δ>0⇔m2>0⇔m≠0.
Khi đó áp dụng định lí Vi-ét ta có: {x1+x2=−ba=m+2x1.x2=ca=m+1⎧⎪ ⎪⎨⎪ ⎪⎩x1+x2=−ba=m+2x1.x2=ca=m+1
Do hai nghiệm phân biệt x1,x2x1,x2 là độ dài hai cạnh góc vuông nên ta có: x1,x2>0x1,x2>0 suy ra:
{x1+x2>0x1.x2>0⇔{m+2>0m+1>0⇔{m>−2m>−1⇔m>−1{x1+x2>0x1.x2>0⇔{m+2>0m+1>0⇔{m>−2m>−1⇔m>−1.
Vì x1,x2x1,x2 là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài đường cao kẻ từ đỉnh góc vuông xuống cạnh huyền là h=2√5h=2√5 nên áp dụng hệ thức lượng trong tam giác vuông ta có:
1x21+1x22=1(2√5)21x21+1x22=1(2√5)2 ⇔x22+x21x21.x22=54⇔x22+x21x21.x22=54
⇔4(x21+x22)=5x21x22⇔4(x1+x2)2−8x1x2=5(x1x2)2⇒4(m+2)2−8(m+1)=5(m+1)2⇔4m2+16m+16−8m−8−5m2−10m−5=0⇔−m2−2m+3=0⇔m2+2m−3=0(∗)⇔4(x21+x22)=5x21x22⇔4(x1+x2)2−8x1x2=5(x1x2)2⇒4(m+2)2−8(m+1)=5(m+1)2⇔4m2+16m+16−8m−8−5m2−10m−5=0⇔−m2−2m+3=0⇔m2+2m−3=0(∗)
Ta có: a+b+c=1+2+(−3)=0a+b+c=1+2+(−3)=0 nên phương trình (*) có 2 nghiệm phân biệt [m=1(tm)m=ca=−3(ktm)⎡⎣m=1(tm)m=ca=−3(ktm).
Vậy m=1m=1 là giá trị cần tìm.
Câu 4 (VDC):
Phương pháp:
a) Vận dụng dấu hiệu: Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau là tứ giác nội tiếp, cụ thể chứng minh ∠OHM=∠OCM=900∠OHM=∠OCM=900 cùng nhìn cạnh OMOM dưới một góc không đổi.
b) + OM⊥CDOM⊥CD tại KK.
+ Áp dụng hệ thức lượng trong tam giác vuông OMDOMD, suy ra OD2=OK.OM=R2OD2=OK.OM=R2
c) + ΔMPQΔMPQ cân tại MM⇒MO⇒MO đồng thời là trung tuyến của ΔMPQΔMPQ⇒OP=12PQ⇒OP=12PQ
+ Tính được SΔMPQ=OM.OPSΔMPQ=OM.OP
+ Áp dụng hệ thức lượng trong tam giác OMPOMP vuông tại OO có 1OM2+1OP2=1OC2=1R21OM2+1OP2=1OC2=1R2
+ Áp dụng BĐT Cô-si cho hai số dương 1OM21OM2 và 1OP21OP2 tìm được giá trị nhỏ nhất của SΔMPQSΔMPQ
Cách giải:
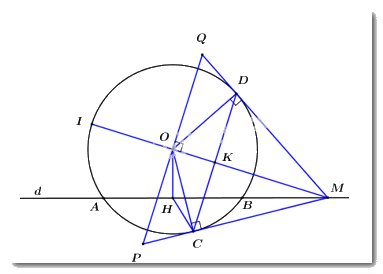
a) Vì HH là trung điểm của AB(gt)AB(gt) ⇒OH⊥AB⇒OH⊥AB (quan hệ vuông góc giữa đường kính và dây cung).
⇒∠OHM=900⇒∠OHM=900.
Xét tứ giác OMCHOMCH có ∠OHM=∠OCM=900∠OHM=∠OCM=900 ⇒OMCH⇒OMCH là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
b) Vì MC=MDMC=MD (tính chất 2 tiếp tuyến cắt nhau) ⇒M⇒M thuộc trung trực của CDCD.
OC=OD(=R)OC=OD(=R) nên OO thuộc trung trực của CDCD.
⇒OM⇒OM là trung trực của CDCD ⇒OM⊥CD⇒OM⊥CD tại KK.
Xét tam giác OMDOMD vuông tại DD có đường cao DKDK ta có: OD2=OK.OM=R2OD2=OK.OM=R2 (hệ thức lượng trong tam giác vuông).
c) Ta có: MOMO là phân giác của ∠PMQ∠PMQ (tính chất 2 tiếp tuyến cắt nhau).
MOMO là đường cao của ΔPMQΔPMQ (do PQ⊥OM(gt)PQ⊥OM(gt))
⇒ΔMPQ⇒ΔMPQ cân tại MM (tam giác có đường cao đồng thời là đường phân giác).
⇒MO⇒MO đồng thời là trung tuyến của ΔMPQΔMPQ ⇒O⇒O là trung điểm của PQPQ ⇒OP=12PQ⇒OP=12PQ.
Ta có SΔMPQ=12MO.PQ=OM.OPSΔMPQ=12MO.PQ=OM.OP.
Áp dụng hệ thức lượng trong tam giác OMPOMP vuông tại OO có đường cao OCOC ta có:
1OM2+1OP2=1OC2=1R21OM2+1OP2=1OC2=1R2.
Áp dụng BĐT Cô-si cho hai số dương 1OM2 và 1OP2 ta có:
1OM2+1OP2≥2OM.OP=2SΔMPQ⇒1R2≥2SΔMPQ⇔SΔMPQ≥2R2
Dấu “=” xảy ra ⇔{OM=OP2OM2=1R2⇔{OM=OPOM=R√2.
Vậy SΔMPQ đạt giá trị nhỏ nhất bằng 2R2 khi OM=R√2.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365