Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 1 Toán 9 Cánh diều - Đề số 1
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau: Câu 1: Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn?
Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn?
2x+3y=5.
0x+2y=8.
2x−0y=5.
0x−0y=6.
Đáp án : D
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng ax+by=c, trong đó a, b và c là các số đã biết (a≠0 hoặc b≠0).
Phương trình 0x−0y=6 là phương trình bậc nhất vì hệ số a=b=0.
Đáp án D.
Hệ phương trình {2x+y=2x+y=1 có nghiệm là:
(x;y)=(0;0).
(x;y)=(1;0).
(x;y)=(1;1).
(x;y)=(−1;−1).
Đáp án : B
Hệ phương trình có nghiệm là cặp số (x0;y0) nếu (x0;y0) là nghiệm của hai phương trình của hệ.
Hệ phương trình {2x+y=2x+y=1 có nghiệm là (x;y)=(1;0) vì {2.1+0=21+0=1.
Đáp án B.
Người ta cần chở một số lượng hàng. Nếu xếp vào mỗi xe 12 tấn thì thừa 3 tấn, nếu xếp vào mỗi xe 15 tấn thì có thể chở thêm 12 tấn nữa. Gọi x là số hàng cần vận chuyển và y là số xe tham gia chở hàng. Hệ phương trình thỏa mãn là:
{x+12y=3x−15y=12.
{x−12y=3−x+15y=12.
{x−12y=3x+15y=12.
{x+12y=3−x+15y=12.
Đáp án : B
Dựa vào đề bài để viết hệ phương trình thỏa mãn đề bài.
Vì nếu xếp mỗi xe 12 tấn thì thừa 3 tấn nên ta có phương trình x−12y=3.
Vì nếu xếp vào mỗi xe 15 tấn thì có thể chở thêm 12 tấn nữa nên ta có phương trình 15y−x=12 hay −x+15y=12.
Vậy hệ phương trình thỏa mãn là {x−12y=3−x+15y=12.
Đáp án B.
Biến đổi phương trình x2−4x+3=0 về phương trình tích, ta được:
(x+1)(x−3)=0.
(x+1)(x+3)=0.
(x−1)(x−3)=0.
(x−1)(x+3)=0.
Đáp án : C
Phân tích vế trái thành nhân tử để biến đổi phương trình về phương trình tích.
Ta có:
x2−4x+3=0x2−x−3x+3=0(x2−x)−(3x−3)=0x(x−1)−3(x−1)=0(x−3)(x−1)=0
Đáp án C.
Hệ thức 2a≤a+1 là một bất đẳng thức và
a+1 là vế trái, 2a là vế phải.
a+1 là vế trước, 2a là vế sau.
a+1 là vế sau, 2a là vế trước.
2a là vế trái, a+1 là vế phải.
Đáp án : D
Ta gọi hệ thức dạng a>b (hay a<b, a≥b, a≤b) là bất đẳng thức và gọi a là vế trái, b là vế phải của bất đẳng thức
Hệ thức 2a≤a+1 có 2a là vế trái, a+1 là vế phải.
Đáp án D.
Khẳng định nào sau đây là khẳng định đúng:
a<b và c>d thì a+b<c+d.
a<b và c<d thì a+c<b+d.
a>b và c>d thì ac>bd.
a>b và c>d thì a+c<b+d.
Đáp án : B
Dựa vào các tính chất của bất đẳng thức.
Theo tính chất liên hệ giữa thứ tự và phép cộng, với a<b và c<d thì a+c<b+d nên đáp án B đúng.
Đáp án B.
Bất phương trình dạng ax+b>0 (hoặc ax+b<0, ax+b≥0, ax+b≤0) là bất phương trình bậc nhất một ẩn (ẩn là x) với điều kiện:
a, b là hai số đã cho.
a, b là hai số đã cho và a≠0.
a≠0.
a và b khác 0.
Đáp án : B
Bất phương trình dạng ax+b<0 (hoặc ax+b>0; ax+b≤0; ax+b≥0) trong đó a, b là hai số đã cho, a≠0 được gọi là bất phương trình bậc nhất một ẩn x.
Điều kiện của a, b là a, b là hai số đã cho và a≠0.
Đáp án B.
Nghiệm của bất phương trình x−2>0 là:
x>2.
x<2.
x<−2.
x>−2.
Đáp án : A
Giải bất phương trình để tìm nghiệm.
Ta có:
x−2>0x>2
Đáp án A.
Cho α và β là hai góc phụ nhau, khi đó:
sinα=cosβ.
sinα=cotβ.
sinα=tanβ.
cosα=cotβ.
Đáp án : A
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Với α và β là hai góc phụ nhau thì sinα=cosβ;tanα=cotβ nên đáp án A đúng.
Đáp án A.
Cho α là góc nhọn bất kì có tanα=15, khi đó cotα bằng:
15.
−15.
5.
−5.
Đáp án : C
Sử dụng kiến thức cotα=1tanα.
Ta có: cotα=1tanα=115=5.
Đáp án C.
Cho tam giác ABC vuông tại B có ˆA=45∘, AC=√2. Độ dài cạnh BC là:
BC=3.
BC=2.
BC=√2.
BC=1.
Đáp án : D
Biểu diễn BC theo AC và tỉ số lượng giác của góc A.
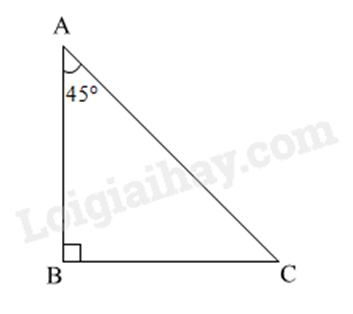
Ta có: sinA=BCAC suy ra BC=AC.sinA=√2.sin45∘=1.
Đáp án D.
Cho tam giác ABC vuông tại A có AB = 5, BC = 8. Số đo góc C là: (làm tròn đến độ)
ˆC≈52∘.
ˆC≈38∘.
ˆC≈51∘.
ˆC≈39∘.
Đáp án : D
Biểu diễn tỉ số lượng giác của góc C theo AB và BC.
Sử dụng máy tính cầm tay để tính góc C theo tỉ số lượng giác của nó.
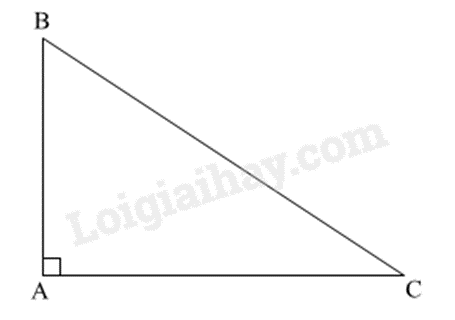
Ta có: sinC=58 suy ra ˆC≈39∘.
Đáp án D.
Giải các phương trình và bất phương trình sau:
a) (x−1)(3x−6)=0
b) 2x+3−1x−2=2x−13(x+3)(x−2)
c) 2x−4>0
d) 2−3x≤4x+5
a) Để giải phương trình tích (ax+b)(cx+d)=0, ta giải hai phương trình ax+b=0 và cx+d=0. Sau đó lấy tất cả các nghiệm của chúng.
b) Tìm điều kiện xác định, quy đồng mẫu và giải phương trình tìm được. Sau đó kiểm tra điều kiện của các nghiệm tìm được.
c, d) Dựa vào cách giải bất phương trình bậc nhất một ẩn và phương trình đưa về dạng bất phương tình bậc nhất một ẩn.
a) (x−1)(3x−6)=0
+) x−1=0
x=1
+) 3x−6=0x=1
3x=6
x=2
Vậy phương trình có nghiệm là x=1; x=2.
b) 2x+3−1x−2=2x−13(x+3)(x−2)
ĐKXĐ: x≠−3 và x≠2.
Ta có:
2x+3−1x−2=2x−13(x+3)(x−2)2x+3−1x−2=2x−13(x+3)(x−2)2(x−2)(x+3)(x−2)−x+3(x+3)(x−2)=2x−13(x+3)(x−2)2(x−2)−(x+3)=2x−132x−4−x−3=2x−13x−7=2x−13x−2x=−13+7−x=−6x=6(TM)
Vậy phương trình có nghiệm là x=6.
c) 2x−4>0
2x>4x>2
Vậy bất phương trình có nghiệm là x>2.
d) 2−3x≤4x+5
−3x−4x≤5−2−7x≤3x≥−37
Vậy bất phương trình có nghiệm là x≥−37.
a) Giải hệ phương trình: {3x−2y=52x+y=1.
b) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Hai xí nghiệp theo kế hoạch phải làm tổng cộng 360 công cụ. Nhờ sắp xếp hợp lý dấy chuyền sản xuất nên xí nghiệp I đã vượt mức 12% kế hoạch, xí nghiệp II đã vượt mức 10% kế hoạch. Do đó cả xí nghiệp đã làm được 400 công cụ. Tính số công cụ mỗi xí nghiệp phải làm theo kế hoạch.
a) Sử dụng phương pháp cộng đại số để giải hệ phương trình.
b) - Đặt ẩn và đặt điều kiện cho ẩn, lập hai phương trình biểu diễn mối quan hệ giữa các ẩn, đưa về bài toán giải hệ phương trình bậc nhất hai ẩn.
- Giải hệ phương trình tìm được ẩn, sau đó kiểm tra điều kiện và chọn giá trị thỏa mãn.
a) Ta có:
{3x−2y=52x+y=1{3x−2y=54x+2y=2{7x=72x+y=1{x=12.1+y=1{x=1y=−1
Vậy hệ phương trình có nghiệm là (x;y)=(1;−1).
b) Gọi số dụng cụ mà xí nghiệp 1 và xí nghiệp II phải làm lần lượt là x,y (x,y∈N∗).
Theo kế hoạch, hai xí nghiệp sản xuất phải làm tổng cộng 360 dụng cụ nên ta có:
x+y=360 (1)
Thực tế, xí nghiệp I đã vượt mức 12% kế hoạch, xí nghiệp II đã vượt mức 10% kế hoạch, do đó hai xí nghiệp đã làm được 400 dụng cụ nên ta có phương trình:
(x+12%x)+(y+10%y)=400 hay 1,12x+1,1y=400 (2)
Từ (1) và (2) ta có hệ phương trình: {x+y=3601,12x+1,1y=400.
Giải hệ phương trình ta được: {x=200y=160(TM).
Vậy theo kế hoạch xí nghiệp I làm được 200 dụng cụ và xí nghiệp II làm được 160 dụng cụ.
Tượng đài chiến thắng là một công trình kiến trúc độc đáo được thi công nhằm kỷ niệm ngày giải phóng thị xã Long Khánh, ngày 21/04/1975 – thể hiện ý chí quyết thắng của quân và dân ta. Em hãy tính chiều cao của công trình này biết rằng khi tia nắng của mặt trời tạo với mặt đất một góc 52∘ thì bóng của nó trên mặt đất là 16m. (Làm tròn đến số thập phân thứ hai). (Giả sử chu vi mặt đáy khối chóp tam giác không đáng kể)

Dựa vào kiến thức về tỉ số lượng giác để tính chiều cao của công trình.
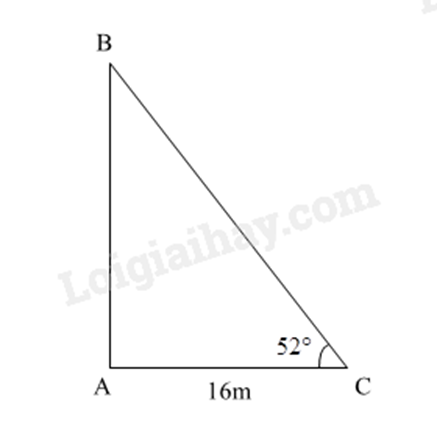
Giả sử hình biểu diễn như hình vẽ.
Xét tam giác ABC vuông tại A, ta có: tanBCA=ABAC
Suy ra AB=AC.tanBCA=16.tan52∘≈20,48(m)
Vậy chiều cao của công trình này là khoảng 20,48m.
Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB=2√3cm; AC=6cm. Giải tam giác ABC.
b) Gọi D, E lần lượt là hình chiếu của điểm H trên AB, AC. Chứng minh BD.DA+CE.EA=AH2.
c) Lấy điểm M nằm giữa E và C, kẻ AI vuông góc với MB tại I.
Chứng minh sin^AMB.sin^ACB=HICM.
a) Vận dụng các kiến thức về hệ thức lượng trong tam giác vuông để giải tam giác.
b) Chứng minh ΔBHD∽ΔHAD(g.g) suy ra BD.DA=DH2
Chứng minh ΔCHE∽ΔHAE(g.g) suy ra CE.AE=HE2.
BD.DA+CE.AE=DH2+HE2
Chứng minh tứ giác ADHE là hình chữ nhật nên AH=DE.
Áp dụng định lí Pythagore vào tam giác DHE vuông tại H, ta có: DH2+HE2=DE2.
Suy ra DH2+HE2=AH2
Từ đó ta có BD.DA+CE.AE=AH2 (đpcm)
c) Chứng minh ΔBIA∽ΔBAM(g.g) suy ra BI.BM=AB2.
Chứng minh ΔBHA∽ΔBAC(g.g) suy ra BH.BC=AB2.
Do đó BI.BM=BH.BC hay BIBC=BHBM.
Chứng minh ΔBHI∽ΔBMC suy ra HIMC=BIBC.
Dựa vào kiến thức về tỉ số lượng giác, ta có: sin^AMB=ABBM; sin^ACB=ABBC.
Biến đối sin^AMB.sin^ACB=ABBM.ABBC=AB2BM.BC=BIBC=HICM. Ta được điều phải chứng minh.
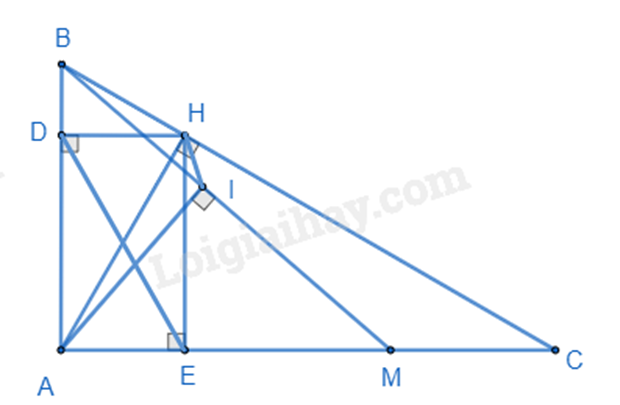
a) Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore trong tam giác, ta có:
BC2=AB2+AC2=(2√3)2+62=48 suy ra BC=√48=4√3(cm)
Ta có: sinB=ACBC=64√3=√32 suy ra ˆB=60∘.
ˆC=90∘−ˆB=90∘−60∘=30∘.
Vậy BC=4√3cm;ˆB=60∘;ˆC=30∘.
b) Xét tam giác BHD và tam giác HAD có:
^BDH=^HDA(=90∘)
^BHD=^HAD (cùng phụ với ^DBH)
suy ra ΔBHD∽ΔHAD(g.g) nên BDDH=DHDA. Do đó BD.DA=DH2. (1)
Xét tam giác CHE và tam giác HAE có:
^CEH=^HEA(=90∘)
^CHE=^HAE (cùng phụ với ˆC)
suy ra ΔCHE∽ΔHAE(g.g) nên CEHE=HEAE. Do đó CE.AE=HE2. (2)
Từ (1) và (2) suy ra BD.DA+CE.AE=DH2+HE2 (3).
Vì tứ giác ADHE có ^DAE=^ADH=^AEH=90∘ nên tứ giác ADHE là hình chữ nhật. Do đó AH=DE.
Áp dụng định lí Pythagore vào tam giác DHE vuông tại H, ta có: DH2+HE2=DE2. Suy ra DH2+HE2=AH2 (4)
Từ (3) và (4) suy ra BD.DA+CE.AE=AH2 (đpcm)
c) Xét tam giác BIA và tam giác BAM có:
^BIA=^BAM(=90∘)
ˆB chung
suy ra ΔBIA∽ΔBAM(g.g) nên BIAB=ABBM. Do đó BI.BM=AB2.
Xét tam giác BHA và tam giác BAC có:
^BHA=^BAC(=90∘)
ˆB chung
suy ra ΔBHA∽ΔBAC(g.g) nên BHAB=ABBC. Do đó BH.BC=AB2.
Từ đó ta có BI.BM=BH.BC suy ra BIBC=BHBM.
Xét tam giác BHI và tam giác BMC có:
ˆB chung
BIBC=BHBM (cmt)
nên ΔBHI∽ΔBMC (c.g.c) suy ra HIMC=BIBC.
Xét tam giác AMB vuông tại A, ta có: sin^AMB=ABBM.
Xét tam giác ABC vuông tại A, ta có: sin^ACB=ABBC.
Suy ra sin^AMB.sin^ACB=ABBM.ABBC=AB2BM.BC=BI.BMBM.BC=BIBC=HICM.
Vậy sin^AMB.sin^ACB=HICM (đpcm).
Một lão nông chia đất cho con trai để người con canh tác riêng, biết rằng người con sẽ được chọn miếng đất hình chữ nhật có chu vi 800 m. Hỏi anh ta phải chọn mảnh đất có kích thước như thế nào để diện tích đất canh tác là lớn nhất.
(HD: Sử dụng bất đẳng thức ab≤(a+b)24).
Gọi hai cạnh của miếng đất là x, y.
Sử dụng bất đẳng thức: ab≤(a+b)24.
* Chứng minh bất đẳng thức ab≤(a+b)24 hay (a+b)2−4ab≥0
Ta có: (a+b)2−4ab≥0 với mọi a, b.
Vậy ab≤(a+b)24.
* Áp dụng bất đẳng thức trên để giải.
Gọi hai cạnh của miếng đất lần lượt là x, y (m). (0<x,y<800)
Vì chu vi của mảnh đất là 800m nên ta có: 2(x+y)=800 hay x+y=800.
Diện tích đất canh tác là xy.
Ta có: xy≤(x+y)24≤40024=40000(m2).
Dấu “=” xảy ra là giá trị lớn nhất của xy. Khi đó kích thước của mảnh đất thỏa mãn x+y=400 và xy=40000.
Ta có x+y=400 nên y=400−x.
Thay vào xy=40000, ta được:
(400−x)x=40000−x2+400x−40000=0x2−400x+40000=0(x−200)2=0x=200
Khi đó y=400−200=200.
Vậy người đó phải chọn mảnh đất có kích thước 200m x 200m để diện tích đất canh tác là lớn nhất.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365