Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 1 Toán 8 Cánh diều
Đề thi giữa kì 1 Toán 8 Cánh diều - Đề số 8
Đề cương ôn tập học kì 1 Toán 8 - Cánh diều Đề thi giữa kì 1 Toán 8 Cánh diều - Đề số 7 Đề thi giữa kì 1 Toán 8 Cánh diều - Đề số 6 Đề thi giữa kì 1 Toán 8 - Đề số 5 - Cánh diều Đề thi giữa kì 1 Toán 8 - Đề số 4 - Cánh diều Đề thi giữa kì 1 Toán 8 - Đề số 3 - Cánh diều Đề thi giữa kì 1 Toán 8 - Đề số 2 - Cánh diều Đề thi giữa kì 1 Toán 8 - Đề số 1 - Cánh diềuĐề thi giữa kì 1 Toán 8 Cánh diều - Đề số 8
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Trong các biểu thức đại số sau, biểu thức nào không phải đơn thức?
22.
x3y2x3y2.
5x+95x+9.
xx.
Đáp án : C
Dựa vào khái niệm đơn thức: Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.
Biểu thức 5x+95x+9 không phải là đơn thức.
Đáp án C.
Tìm hệ số trong đơn thức 13ab2xy13ab2xy với a, b là hằng số
1313.
13a2b13a2b.
13ab213ab2.
xyxy.
Đáp án : C
Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.
Vì a, b là hằng số nên hệ số trong đơn thức là 13ab213ab2.
Đáp án C.
Tất cả các hạng tử của đa thức B=3x2−2x+1B=3x2−2x+1 là
3x23x2; −2x−2x và 1.
3x23x2 và −2x−2x.
33; −2−2 và 1.
−2x−2x và 1.
Đáp án : A
Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Các hạng tử của đa thức là: 3x23x2; −2x−2x và 1.
Đáp án A.
Trong các đơn thức sau, đơn thức nào đồng dạng với đơn thức −3x2yz−3x2yz?
−3xyz−3xyz.
23x2yz23x2yz.
32zx232zx2.
4x2y4x2y.
Đáp án : B
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Đơn thức 23x2yz23x2yz có cùng phần biến x2yzx2yz với đơn thức −3x2yz−3x2yz nên là hai đơn thức đồng dạng.
Đáp án B.
Bậc của đa thức x2y2+xy5−x2y4x2y2+xy5−x2y4 là
7.
6.
5.
4.
Đáp án : B
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức.
Đa thức x2y2+xy5−x2y4x2y2+xy5−x2y4 gồm 3 đơn thức x2y2;xy5;−x2y4x2y2;xy5;−x2y4 với bậc lần lượt là 4;6;64;6;6.
Do đó bậc của đa thức x2y2+xy5−x2y4x2y2+xy5−x2y4 là 6.
Đáp án B.
Điền vào chỗ trống sau: (x+2)2=x2+...+4(x+2)2=x2+...+4
2x2x.
4x4x.
22.
44.
Đáp án : B
Dựa vào hằng đẳng thức bình phương của một tổng.
Ta có: (x+2)2=x2+4x+4(x+2)2=x2+4x+4.
Chỗ trống cần điền là 4x4x.
Đáp án B.
Biểu thức x3+64x3+64 được viết dưới dạng tích là
(x−4)(x2+4x+16)(x−4)(x2+4x+16).
(x−4)(x2+4x−16)(x−4)(x2+4x−16)
(x+4)(x2+4x+16)(x+4)(x2+4x+16).
(x+4)(x2−4x+16)(x+4)(x2−4x+16).
Đáp án : D
Dựa vào hằng đẳng thức tổng hai lập phương.
Ta có:
x3+64=x3+43=(x+4)(x2−4x+16)x3+64=x3+43=(x+4)(x2−4x+16).
Đáp án D.
Kết quả của phép tính (x−3y)(x+3y)(x−3y)(x+3y) là
x2−9y2x2−9y2.
x2−6xy+9y2x2−6xy+9y2.
x2+6xy+9y2x2+6xy+9y2.
x2−9xy+9y2x2−9xy+9y2.
Đáp án : A
Dựa vào hằng đẳng thức hiệu hai bình phương.
Ta có:
(x−3y)(x+3y)=x2−(3y)2=x2−9y2(x−3y)(x+3y)=x2−(3y)2=x2−9y2.
Đáp án A.
Với điều kiện của xx thì phân thức x−36x+24x−36x+24 xác định?
x≠2x≠2.
x≠3x≠3.
x≠−4x≠−4.
x≠4x≠4.
Đáp án : C
Điều kiện của biến để giá trị tương ứng của mẫu thức khác 0 được gọi điều kiện để giá trị của phân thức được xác định.
Phân thức x−36x+24x−36x+24 xác định khi và chỉ khi 6x+24≠06x+24≠0 tức là x≠−4x≠−4.
Đáp án C.
Kết quả của phép tính 2x+1x−3+53−x2x+1x−3+53−x là:
2x+4x−32x+4x−3.
2x−4x−32x−4x−3.
2x+4(x−3)22x+4(x−3)2.
2x+6x−32x+6x−3.
Đáp án : B
Đưa hai phân thức về cùng mẫu để thực hiện phép cộng.
Ta có:
2x+1x−3+53−x=2x+1x−3−5x−3=2x+1−5x−3=2x−4x−32x+1x−3+53−x=2x+1x−3−5x−3=2x+1−5x−3=2x−4x−3.
Đáp án B.
Hình chóp tam giác đều có mặt bên là hình gì?
Tam giác cân.
Tam giác vuông.
Tam giác vuông cân.
Tam giác đều.
Đáp án : A
Dựa vào đặc điểm của hình chóp tam giác đều.
Hình chóp tam giác đều có mặt bên là tam giác cân.
Đáp án A.
Một chậu cây cảnh mini có hình dạng là hình chóp tứ giác đều có cạnh đáy bằng 24cm24cm, chiều cao bằng 35cm35cm. Thể tích của hình chóp bằng

20160cm320160cm3.
840cm3840cm3.
3360cm33360cm3.
6720cm36720cm3.
Đáp án : D
Sử dụng công thức tính thể tích hình chóp: V=S.hV=S.h (S là diện tích đáy, h là chiều cao)
Thể tích của hình chóp là:
V=13.242.35=6720(cm3)V=13.242.35=6720(cm3).
Đáp án D.
Thực hiện phép tính:
a) (2x+3)2(2x+3)2;
b) (15x4y5−30x3y4+5x5y4):(5x3y3)(15x4y5−30x3y4+5x5y4):(5x3y3);
c) (x+3)(x2+3x−5)(x+3)(x2+3x−5).
a) Sử dụng hằng đẳng thức bình phương của một tổng.
b) Sử dụng quy tắc chia đa thức cho đơn thức.
c) Sử dụng quy tắc nhân đa thức với đa thức.
a) (2x+3)2(2x+3)2
=(2x)2+2.2x.3+32=(2x)2+2.2x.3+32
=4x2+12x+9=4x2+12x+9
b) (15x4y5−30x3y4+5x5y4):(5x3y3)(15x4y5−30x3y4+5x5y4):(5x3y3)
=15x4y5:5x3y3−30x3y4:5x3y3+5x5y4:5x3y3=15x4y5:5x3y3−30x3y4:5x3y3+5x5y4:5x3y3
=3xy2−6y+x2y=3xy2−6y+x2y
c) (x+3)(x2+3x−5)(x+3)(x2+3x−5)
=x3+3x2−5x+3x2+9x−15=x3+3x2−5x+3x2+9x−15
=x3+6x2+4x−15=x3+6x2+4x−15
Phân tích đa thức thành nhân tử:
a) 4x2−254x2−25;
b) x(x−7)−3x+21x(x−7)−3x+21.
Sử dụng các phương pháp phân tích đa thức thành nhân tử phù hợp.
a) 4x2−254x2−25
=(2x)2−52=(2x−5)(2x+5)
b) x(x−7)−3x+21
=x(x−7)−3(x−7)=(x−7)(x−3)
Cho biểu thức A=5x−2x2−4−3x+2+xx−2.
a) Tìm điều kiện xác định của biểu thức A.
b) Rút gọn biểu thức A.
c) Tính giá trị của biểu thức A với x thỏa mãn |x+3|=5.
a) Điều kiện của biến để giá trị tương ứng của mẫu thức khác 0 được gọi điều kiện để giá trị của phân thức được xác định.
b) Thực hiện phép tính cộng, trừ với phân thức đại số để rút gọn.
c) Tìm giá trị của x thỏa mãn |x+3|=5.
Kiểm tra điều kiện của x.
Với giá trị x thỏa mãn, thay vào A để tính giá trị.
a) Điều kiện xác định của biểu thức A là:
x2−4≠0, x+2≠0 và x−2≠0. Tức là x≠±2.
b) Với x≠±2, ta có:
A=5x−2x2−4−3x+2+xx−2
=5x−2−3(x−2)+x(x+2)(x+2)(x−2)
=5x−2−3x+6+x2+2x(x+2)(x−2)
=x2+4x+4(x+2)(x−2)
=(x+2)2(x+2)(x−2)=x+2x−2.
c) Ta có: |x+3|=5
x+3=5 hoặc x+3=−5
x=2 (không thỏa mãn) hoặc x=−8 (thỏa mãn)
Thay x=−8 vào biểu thức A=x+2x−2 ta được:
A=−8+2−8−2=−6−10=35.
1. Chiếc hộp (Hình a) được vẽ lại như Hình b có dạng hình chóp tam giác đều S.MNP.
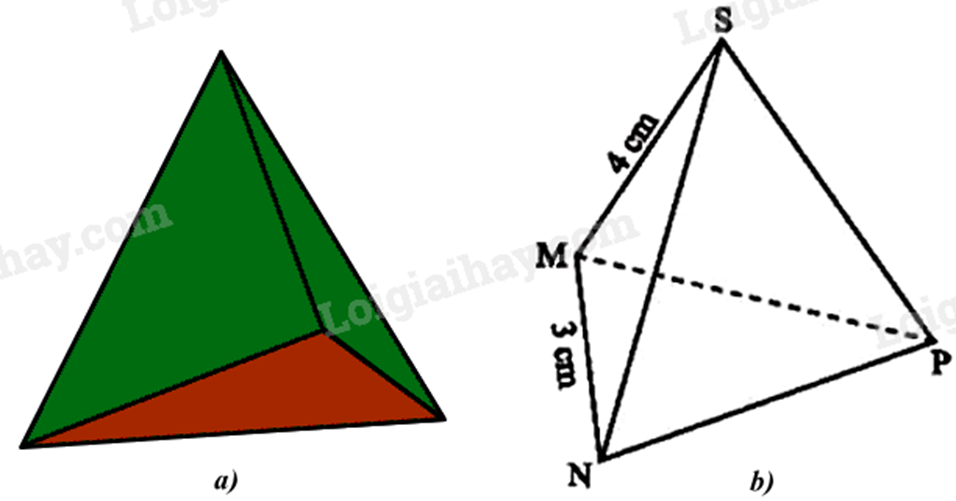
a) Hãy cho biết mặt đáy, mặt bên, cạnh bên của chiếc hộp đó.
b) Cho biết SM = 4cm, MN = 3 cm. Tìm độ dài các cạnh còn lại của chiếc hộp.
2. Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.

a) Cạnh bên của hình chóp là bao nhiêu?
b) Tính thể tích hình chóp.
1. Dựa vào đặc điểm của hình chóp tam giác đều để xác định.
2. a) Sử dụng định lí Pythagore vào tam giác vuông để tính cạnh bên của hình chóp.
b) Sử dụng công thức tính thể tích hình chóp tứ giác đều: V=S.h (S là diện tích đáy, h là chiều cao).
1.
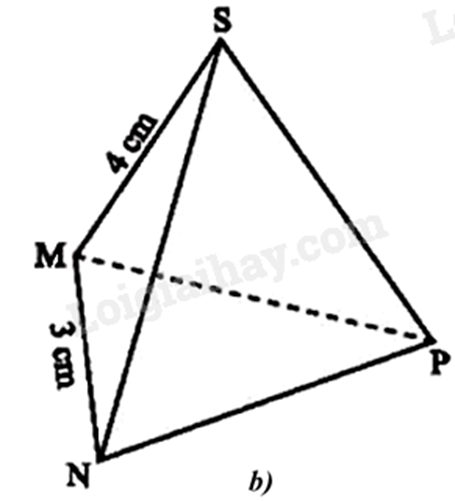
a) Mặt đáy là: (MNP).
Các mặt bên là: (SMN), (SNP), (SMP).
Các cạnh bên là: SM, SN, SP.
b) Độ dài các cạnh còn lại của chiếc hộp là:
SN = SP = SM = 4cm;
NP = MP = MN = 3cm.
2.
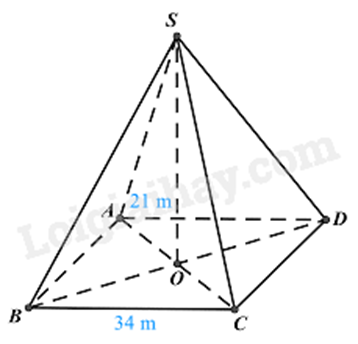
Giả sử kim tự tháp Lu-vrơ (Louvre) là hình chóp tứ giác đều S.ABCD.
Hình chóp tứ giác đều S.ABCD có ABCD là hình vuông nên AC = BD nên AO = OB.
Áp dụng định lí Pythagore vào tam giác vuông AOB, ta có:
AO2+OB2=AB22AO2=342AO2=342:2=1156:2=578
Vì S.ABCD là hình chóp tứ giác đều nên SO⊥AO, suy ra ΔSAO vuông tại O.
Áp dụng định lí Pythagore vào tam giác vuông SAO, ta có:
SA2=SO2+AO2=212+578=1019.
Suy ra SA=√1019≈31,9(m).
b) Thể tích kim tự tháp là:
V=13.342.21=8092(m3).
Một viên bi lăn theo đoạn đường từ A đến D như hình vẽ (AB⊥BC,BC⊥CD). Hãy tính khoảng cách AD. Biết rằng AB = 10m, BC = 12m, CD = 6m.
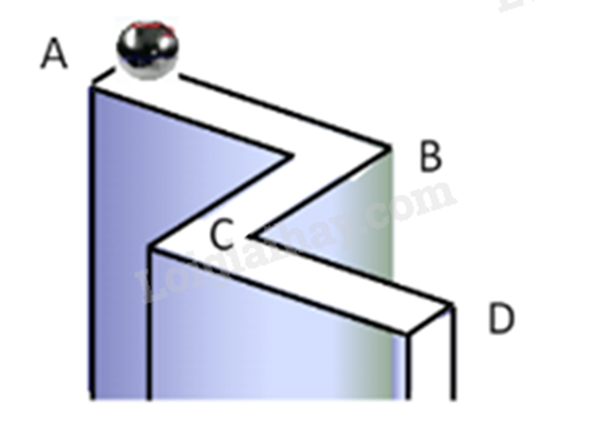
Từ D vẽ Dx⊥CD cắt AB tại E.
Chứng minh BCDE là hình chữ nhật, sử dụng tính chất của hình chữ nhật để tính BE, suy ra độ dài AE.
Dựa vào định lí Pythagore để tính cạnh AD.
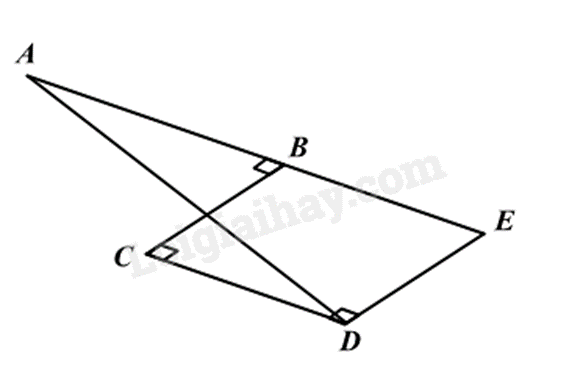
Từ D vẽ Dx⊥CD cắt AB tại E.
Mà BC⊥CD nên DE//BC.
Vì AB⊥BC,BC⊥CD nên AB//CD.
Xét tứ giác BCDE có ˆB=ˆC=ˆD=90∘ nên BCDE là hình chữ nhật.
Suy ra DE=BC=12m; BE=CD=6m; ˆE=90∘.
Dẫn đến AE=AB+BE=10+6=16(m)
Áp dụng định lí Pythagore vào tam giác ADE vuông tại E, ta có:
AD=√AE2+DE2=√162+122=20(m)
Vậy khoảng cách AD là 20m.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365