Chỉ có câu 3. không phải mệnh đề.

A sai vì a là phần tử, không dùng kí hiệu $\subset$.

B đúng.

C sai vì {a} là tập hợp chứa 1 phần tử a, không dùng kí hiệu $\in$.

D sai vì (a;b] là tập hợp không chứa phần tử a.

Thay tọa độ của O(0;0) vào tất cả các bất phương trình trên, chỉ thấy $0 + 3.0 < 0$ là sai.

Vậy O(0;0) không phải là nghiệm của hệ $\left\{ \begin{array}{l}x + 3y < 0\\2x + y + 4 > 0\end{array} \right.$.

Hệ ở đáp án D không là hệ bất phương trình bậc nhất hai ẩn vì hệ này chứa một bất phương
trình bậc hai ${x^2} + 2y \le 15$.

$\sin {150^o} = \frac{1}{2}$; $\cos {150^o} =  - \frac{{\sqrt 3 }}{2}$; $\tan {150^o} =  - \frac{{\sqrt 3 }}{3}$; $\cot {150^o} =  - \sqrt 3$.

Theo định lí Sin: $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$.

Các vecto cùng hướng với $\overrightarrow u$ là $\overrightarrow a$ và $\overrightarrow v$.

Điều kiện xác định của hàm số $y = \frac{x}{{x + 2}}$ là $x + 2 \ne 0$ hay $x \ne 2$.

Vậy tập xác định là $D = \mathbb{R}\backslash \{  - 2\}$.

Đồ thị hàm số bậc hai là một parabol. A sai.

Khi đó, hàm số không thể chỉ đồng biến (đồ thị đi lên từ trái sang) hay nghịch biến (đồ thị đi xuống từ trái sang) nên C, D sai.

Ta có: $\overrightarrow {BA} .\overrightarrow {BC}  = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = BA.BC\cos \widehat {ABC} = a.a\cos {60^o} = \frac{{{a^2}}}{2}$.

Suy ra $\overrightarrow {AB} .\overrightarrow {BC}  =  - \overrightarrow {BA} .\overrightarrow {BC}  =  - \frac{{{a^2}}}{2}$.

Để biểu thức $f(x) = (m - 2){x^2} + 2x - 3$ là một tam thức bậc hai thì $m - 2 \ne 0$ hay $m \ne 2$.

$\sqrt {3{x^2} - 9x + 7}  = x - 2 \Leftrightarrow \left\{ \begin{array}{l}3{x^2} - 9x + 7 = {x^2} - 4x + 4\\x - 2 \ge \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{x^2} - 5x + 3 = 0\\x \ge 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = \frac{3}{2}\\x = 1\end{array} \right.\\x \ge 2\end{array} \right.$

Vậy phương trình vô nghiệm.

a) Đúng. Số tiền phải trả cho cuộc gọi nội mạng mỗi tháng là x (nghìn đồng), số tiền phải trả cho cuộc gọi ngoại mạng mỗi tháng là 2y (nghìn đồng). Điều kiện: $x,y \in \mathbb{N}$.

b) Sai. Vì mỗi tuần Bình chỉ bỏ ra số tiền thấp hơn 100 nghìn đồng nên ta có bất phương trình:

x + 2y < 100.

c) Đúng. Thay cặp số (50;20) vào bất phương trình vừa tìm: $50 + 2.20 < 100$ (đúng).

Vậy trong một tháng, Bình có thể gọi 50 phút nội mạng và 20 phút ngoại mạng mà số tiền phải trả không đến 100 nghìn đồng.

d) Đúng. Vẽ đường thẳng (d): x + 2y = 100 đi qua hai điểm A(0;50) và B(100;0).

Thay tọa độ điểm O(0;0) vào bất phương trình: 0 + 2.0 < 100 (đúng) nên O(0;0) thuộc miền nghiệm.

Vậy miền nghiệm của x + 2y < 100 là nửa mặt phẳng (không kể d) chứa điểm O (phần không gạch chéo).

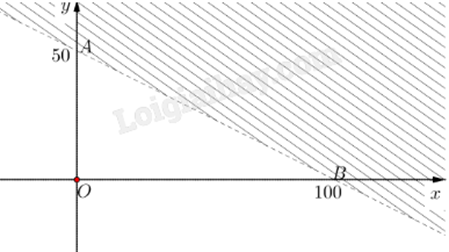
Kết hợp điều kiện $x,y \in \mathbb{N}$ ta có miền nghiệm là miền tam giác OAB.

a) Đúng. $\cos \alpha  = \frac{1}{2} \Rightarrow \alpha  = {60^o}$.

b) Sai. Các góc ${0^o} < \alpha  < {180^o}$ có giá trị sin dương nên với ${0^o} < \alpha  < {90^o}$ thì $\sin \alpha  > 0$.

c) Đúng. ${\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }} - 1 = \frac{1}{{{{\left( {\frac{1}{2}} \right)}^2}}} - 1 = 3$.

d) Sai. Ta có:

$P = 3{\sin ^2}\alpha  + 4{\cos ^2}\alpha  = 3(1 - {\cos ^2}\alpha ) + 4{\cos ^2}\alpha  = 3 + {\cos ^2}\alpha  = 3 + {\left( {\frac{1}{2}} \right)^2} = \frac{{13}}{4}$.

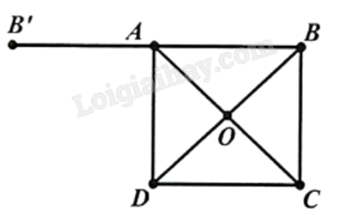
a) Đúng. Vì ABCD là hình vuông nên áp dụng quy tắc hình bình hành, ta có: $\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC}$.

b) Đúng. O là trung điểm của BD nên $\overrightarrow {OD}  = \overrightarrow {BO}$.

Ta có $\left| {\overrightarrow {AB}  + \overrightarrow {OD} } \right| = \left| {\overrightarrow {AB}  + \overrightarrow {BO} } \right| = \left| {\overrightarrow {AO} } \right| = AO$.

c) Đúng. O là trung điểm của AC nên $\overrightarrow {OC}  = \overrightarrow {AO}$.

Ta có $\left| {\overrightarrow {AB}  - \overrightarrow {OC}  + \overrightarrow {OD} } \right| = \left| {\overrightarrow {AB}  - \overrightarrow {AO}  + \overrightarrow {OD} } \right| = \left| {\overrightarrow {AB}  + \overrightarrow {OA}  + \overrightarrow {OD} } \right| = \left| {\overrightarrow {OB}  + \overrightarrow {OD} } \right| = \left| {\overrightarrow 0 } \right| = 0$.

d) Sai. Gọi B’ là điểm đối xứng với B qua A. Khi đó B’ cố định và $\overrightarrow {BB'}  = 2\overrightarrow {BA}$.

$\left| {\overrightarrow {MA}  - \overrightarrow {MB}  - \overrightarrow {MC}  + \overrightarrow {MD} } \right| = \left| {\left( {\overrightarrow {MA}  - \overrightarrow {MB} } \right) - \left( {\overrightarrow {MC}  + \overrightarrow {MD} } \right)} \right| = \left| {\overrightarrow {BA}  - \overrightarrow {DC} } \right| = \left| {\overrightarrow {BA}  + \overrightarrow {BA} } \right| = \left| {\overrightarrow {BB'} } \right| = BB'$.

Suy ra $BB' = MO$. Vậy tập hợp điểm M là đường tròn tâm O bán kính R = BB’.

Có ${x^2} \ge 0 \Rightarrow 2{x^2} + 1 > 0$ $\forall x \in \mathbb{R}$.

$f(x) = ( - {x^2} + 3x)(2{x^2} + 1) = 0 \Leftrightarrow  - {x^2} + 3x = 0$ (vì $2{x^2} + 1 > 0$ $\forall x \in \mathbb{R}$)

Giải phương trình trên, ta được hai nghiệm x = 0, x = 3.

a) Đúng.

b) Đúng.

c) Sai. Ta có bảng xét dấu:

Theo bảng xét dấu, $f(x) > 0$, $\forall x \in (0;3)$.

d) Sai. Theo bảng xét dấu, $f(x) < 0$, $\forall x \in ( - \infty ;0) \cup (3; + \infty )$.

Điều kiện: $\left\{ \begin{array}{l}m - 1 < 4\\ - 2 < 2m + 2\end{array} \right. \Leftrightarrow  - 2 < m < 5$.

Ta có $A \cap B = \emptyset  \Leftrightarrow \left[ \begin{array}{l}2m + 2 \le m - 1\\4 \le  - 2\end{array} \right. \Leftrightarrow m \le  - 3$.

Suy ra $A \cap B \ne \emptyset  \Leftrightarrow \left\{ \begin{array}{l} - 2 < m < 5\\m >  - 3\end{array} \right. \Leftrightarrow  - 2 < m < 5$.

Các giá trị nguyên m thỏa mãn là -1; 0; 1; 2; 3; 4.

Vậy có 6 giá trị nguyên m thỏa mãn yêu cầu đề bài.

Ta có điều kiện $x,y \ge 0$.

Để sản xuất x sản phẩm I cần 2x máy nhóm A.

Để sản xuất ra y sản phẩm II cần 2y máy nhóm A.

Mà chỉ có 10 máy nhóm A nên $2x + 2y \le 10$.

Tương tự với các máy nhóm B, C và kết hợp điều kiện, ta được hệ bất phương trình:

$\left\{ \begin{array}{l}2x + 2y \le 10\\2y \le 4\\2x + 4y \le 12\\x,y \ge 0\end{array} \right.$ hay $\left\{ \begin{array}{l}x + y \le 5\\y \le 2\\x + 2y \le 6\\x,y \ge 0\end{array} \right.$   (*).

Lợi nhuận thu được là f(x;y) = 30x + 50y (nghìn đồng).

Bài toán trở thành tìm giá trị lớn nhất của f(x;y) trên miền nghiệm của hệ (*).

Miền nghiệm của hệ (*) là miền ngũ giác OABCD (kể cả biên) với $O(0;0)$, $B(4;1)$, $C(2;2)$, $D(0;2)$.

Thay tọa độ các điểm trên vào f(x;y) thấy f(4;1) = 170 là giá trị lớn nhất.

Do đó, cần sản xuất 4 sản phẩm I và 1 sản phẩm II để thu về lợi nhuận cao nhất.

Vậy x – y = 4 – 1 = 3.

+) $\widehat {BAC} + \widehat {DAC} = {90^o}$

$\widehat {BAC} = {90^o} - \widehat {DAC} = {90^o} - {35^o} = {55^o}$.

+) $\widehat {CBA} = \widehat {CBE} + \widehat {ABE} = {15^o} + {90^o} = {105^o}$.

+) Xét tam giác ABC có $\widehat C = {180^o} - \widehat A - \widehat B = {180^o} - {55^o} - {105^o} = {20^o}$.

Áp dụng định lí Sin cho tam giác ABC: $\frac{{AB}}{{\sin \widehat {BCA}}} = \frac{{AC}}{{\sin \widehat {ABC}}}$.

Suy ra $AC = \frac{{AB\sin \widehat {ABC}}}{{\sin \widehat {ACB}}} = \frac{{60\sin {{105}^o}}}{{\sin {{20}^o}}}$.

Xét tam giác ACD vuông tại D: $\sin \widehat {CAD} = \frac{{CD}}{{AC}}$.

Suy ra $CD = AC\sin \widehat {CAD} = \frac{{60\sin {{105}^o}}}{{\sin {{20}^o}}}\sin {35^o} \approx 97,2$.

Dựng hình bình hành OACB sao cho OA = OB = 20, $\widehat {AOC} = \widehat {BOC} = {45^o}$ và $\overrightarrow {OC}$cùng hướng với $\overrightarrow {{F_1}}$.

Khi đó $\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {OA} } \right| = OA = 20$, $\left| {\overrightarrow {{F_4}} } \right| = \left| {\overrightarrow {OB} } \right| = OB = 20$, $\overrightarrow {{F_3}}  + \overrightarrow {{F_4}}  = \overrightarrow {{F_{34}}}  = \overrightarrow {OC}$ và $\left| {\overrightarrow {{F_{34}}} } \right| = \left| {\overrightarrow {OC} } \right|$.

Vì OA = OB nên OACB là hình thoi.

Mà $\widehat {AOB} = \widehat {AOC} + \widehat {COB} = {45^o} + {45^o} = {90^o}$ nên OACB là hình vuông.

Khi đó $OC = \sqrt 2 OA = 20\sqrt 2$.

Vì độ lớn lực $\overrightarrow {{F_2}}$ gấp đôi độ lớn lực $\overrightarrow {{F_1}}$ và hai lực này ngược chiều nên $\overrightarrow {{F_2}}  =  - 2\overrightarrow {{F_1}}$.

Dưới tác động của 4 lực, vật ở vị trí cân bằng nên ta có:

$\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}}  = \overrightarrow 0  \Rightarrow \overrightarrow {{F_1}}  - 2\overrightarrow {{F_1}}  + \overrightarrow {{F_{34}}}  = \overrightarrow 0  \Rightarrow \overrightarrow {{F_{34}}}  = \overrightarrow {{F_1}}  \Rightarrow \left| {\overrightarrow {{F_{34}}} } \right| = \left| {\overrightarrow {{F_1}} } \right| = 20\sqrt 2$.

$\Rightarrow \left| {\overrightarrow {{F_2}} } \right| = 2\left| {\overrightarrow {{F_1}} } \right| = 2.20\sqrt 2  = 40\sqrt 2$.

Vậy $\left| {\overrightarrow {{F_1}} } \right| + \left| {\overrightarrow {{F_2}} } \right| = 20\sqrt 2  + 40\sqrt 2  = 60\sqrt 2  \approx 84,9$ (N).

Lợi nhuận của xí nghiệp khi bán hết Q sản phẩm là:

$1200Q - ({Q^2} + 300Q + 200000) =  - {Q^2} + 900Q - 200000$.

Để xí nghiệp không bị lỗ thì $- {Q^2} + 900Q - 200000 \ge 0 \Leftrightarrow 400 \le Q \le 500$.

Do đó, để không bị lỗ, xí nghiệp cần sản xuất nhiều hơn hoặc bằng 400 sản phẩm và ít hơn hoặc bằng 500 sản phẩm.

Vậy a + b = 400 + 500 = 900.

Dựng hệ trục Oxy như hình vẽ và gọi hàm số tương ứng với cổng Arch là $y = a{x^2} + bx + c$ $(a \ne 0)$.

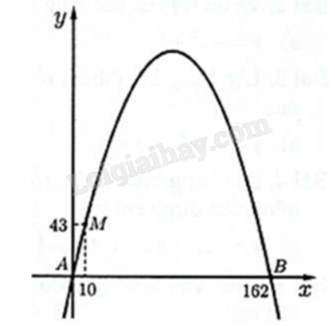
Vì parabol đi qua ba điểm A(0;0), B(162;0), C(10;43) nên ta thay tọa độ các điểm trên vào hàm số:

$\left\{ \begin{array}{l}c = 0\\{162^2}a + 162b + c = 0\\{10^2}a + 10b + c = 43\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - \frac{{43}}{{1520}}\\b = \frac{{3483}}{{760}}\end{array} \right.$

Từ đó ta xác định được hàm số $y =  - \frac{{43}}{{1520}}{x^2} + \frac{{3483}}{{760}}x$.

Đỉnh I của parabol có tọa độ ${x_I} =  - \frac{b}{{2a}} = 81$, ${y_I} =  - \frac{{43}}{{1520}}{.81^2} + \frac{{3483}}{{760}}.81 \approx 185,6$ (m).