Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 21. Đường tròn trong mặt phẳng tọa độ Toán 10 Kết nối tri thức
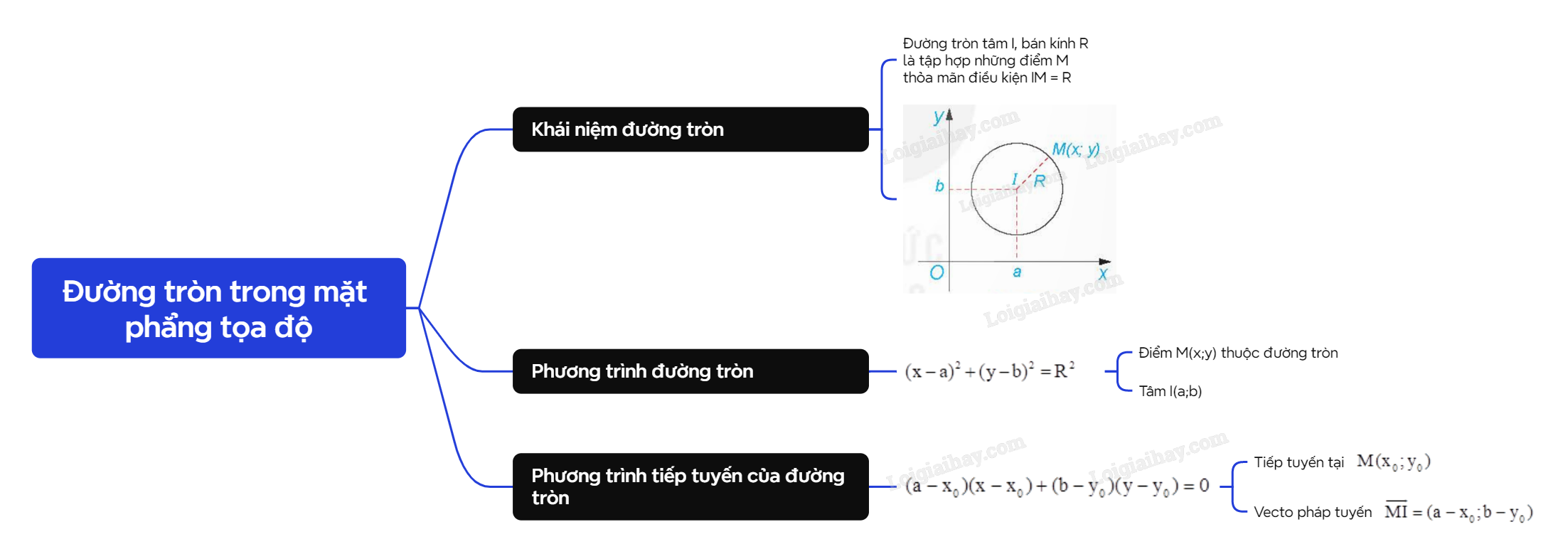
Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Kết nối tri thức
Giải mục 1 trang 43, 44, 45 SGK Toán 10 tập 2 - Kết nối tri thức Giải mục 2 trang 46 SGK Toán 10 tập 2 - Kết nối tri thức Giải bài 7.13 trang 46 SGK Toán 10 – Kết nối tri thức Giải bài 7.15 trang 47 SGK Toán 10 – Kết nối tri thức Giải bài 7.16 trang 47 SGK Toán 10 – Kết nối tri thức Giải bài 7.17 trang 47 SGK Toán 10 – Kết nối tri thức Giải bài 7.18 trang 47 SGK Toán 10 – Kết nối tri thứcLý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Kết nối tri thức
A. Lý thuyết 1. Phương trình đường tròn Đường tròn tâm I, bán kính R là tập hợp những điểm M thỏa mãn điều kiện IM = R. Do đó, để lập phương trình đường tròn, ta cần chuyển điều kiện hình học IM = R thành một điều kiện đại số.
A. Lý thuyết
1. Phương trình đường tròn
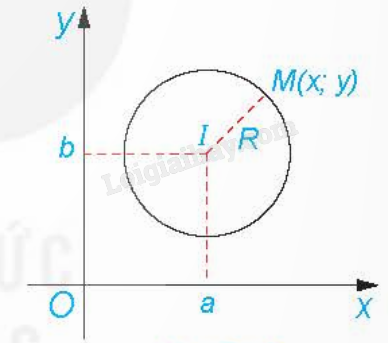
Đường tròn tâm I, bán kính R là tập hợp những điểm M thỏa mãn điều kiện IM = R. Do đó, để lập phương trình đường tròn, ta cần chuyển điều kiện hình học IM = R thành một điều kiện đại số.
|
Điểm M(x;y) thuộc đường tròn (C), tâm I(a;b), bán kính R khi và chỉ khi . Phương trình trên là phương trình đường tròn (C). |
Nhận xét: Phương trình là phương trình của một đường tròn (C) khi và chỉ khi . Khi đó, (C) có tâm I(a;b) và bán kính .
2. Phương trình tiếp tuyến của đường tròn
|
Cho điểm thuộc đường tròn (C): (tâm I(a;b), bán kính R). Khi đó, tiếp tuyến của (C) tại có vecto pháp tuyến và phương trình . |
B. Bài tập
Bài 1:
a) Tìm tâm và bán kính đường tròn (C) có phương trình: .
b) Viết phương trình đường tròn (C’) tâm J(2;-1) và có bán kính gấp đôi bán kính đường tròn (C).
Giải:
a) Ta viết phương trình của (C) ở dạng .
Vậy (C) có tâm I(2;-3) và bán kính R = 4.
b) Đường tròn (C’) có tâm J(2;-1) và bán kính R’ = 2R = 8 nên có phương trình:
.
Bài 2: Phương trình có phải là phương trình đường tròn không? Nếu có, xác định tọa độ tâm và bán kính của đường tròn đó.
Giải:
Từ phương trình, ta có ; ; c = -4.
Suy ra .
Vậy phương trình là phương trình đường tròn tâm I(2;-1) và bán kính .
Bài 3: Lập phương trình đường tròn đi qua ba điểm A(-1;1), B(0;-2), C(0;2).
Giải:
Giả sử tâm của đường tròn là điểm I(a;b). Ta có .
Khi đó:
.
Đường tròn tâm I(1;0) bán kính .
Phương trình đường tròn là .
Vậy phương trình đường tròn là .
Bài 4: Cho đường tròn (C) có phương trình . Điểm M(0;1) có thuộc đường tròn (C) hay không? Nếu có, hãy viết phương trình tiếp tuyến tại M của (C).
Giải:
Do , nên điểm M thuộc (C).
Đường tròn (C) có tâm là I(-1;3). Tiếp tuyến của (C) tại M(0;1) có vecto pháp tuyến .
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365