Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 2. Biểu thức tọa độ của các phép toán vectơ Toán 10 Cánh diều
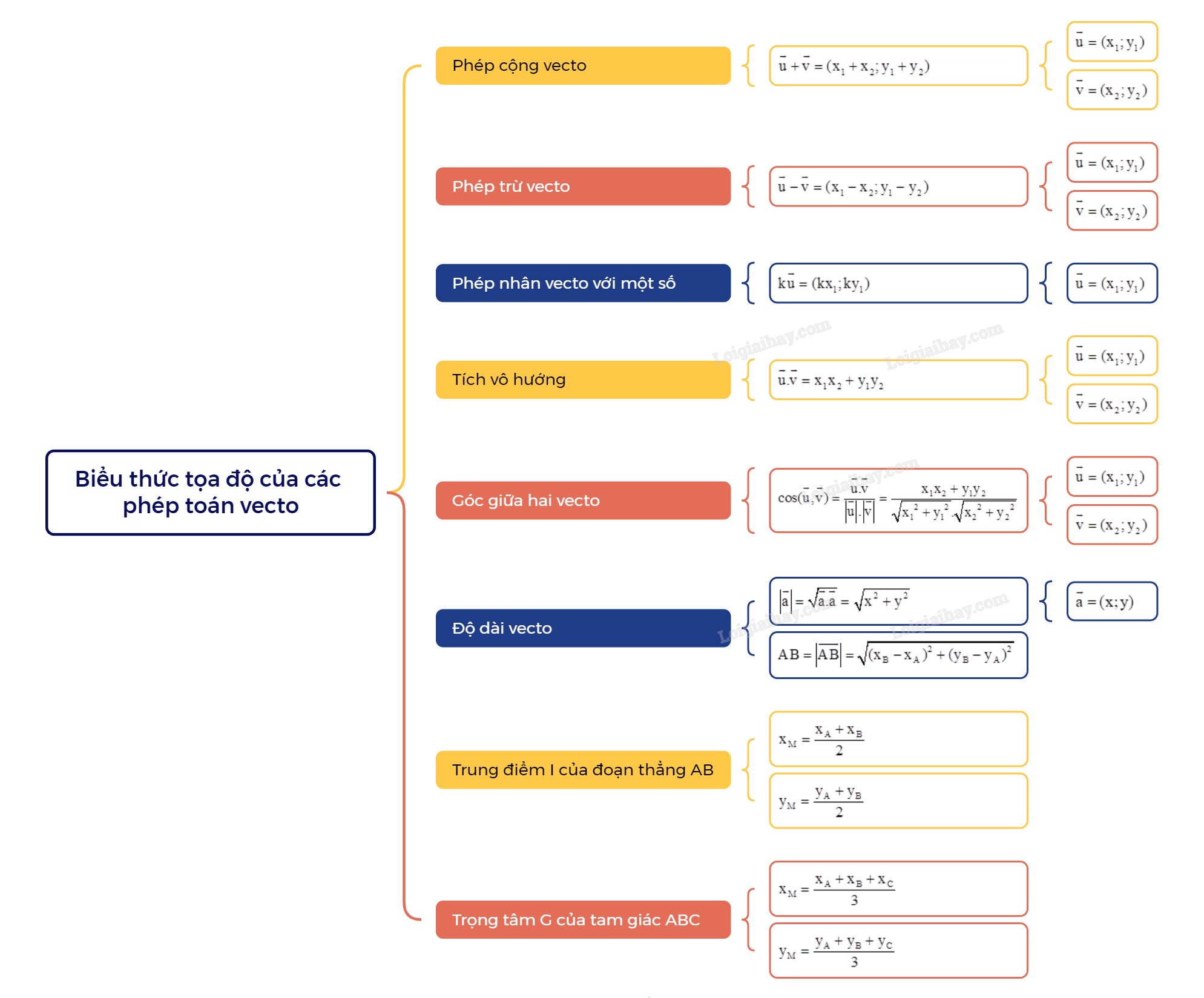
Lý thuyết Biểu thức tọa độ của các phép toán vecto - SGK Toán 10 Cánh diều
Giải mục I trang 67, 68 SGK Toán 10 tập 2 - Cánh diều Giải mục II trang 69 SGK Toán 10 tập 2 - Cánh diều Giải mục III trang 70 SGK Toán 10 tập 2 - Cánh diều Giải bài 1 trang 72 SGK Toán 10 tập 2 – Cánh diều Giải bài 2 trang 72 SGK Toán 10 tập 2 – Cánh diều Giải bài 3 trang 72 SGK Toán 10 tập 2 – Cánh diều Giải bài 4 trang 72 SGK Toán 10 tập 2 – Cánh diều Giải bài 5 trang 72 SGK Toán 10 tập 2 – Cánh diều Giải bài 6 trang 72 SGK Toán 10 tập 2 – Cánh diều Giải bài 7 trang 72 SGK Toán 10 tập 2 – Cánh diềuLý thuyết Biểu thức tọa độ của các phép toán vecto - SGK Toán 10 Cánh diều
A. Lý thuyết 1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
A. Lý thuyết
1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
|
Nếu và thì: + . + . + với . |
Nhận xét: Hai vecto và cùng phương khi và chỉ khi có một số thực k sao cho và .
2. Tọa độ trung điểm đoạn thẳng và tọa độ trọng tâm tam giác
a) Tọa độ trung điểm đoạn thẳng
| Cho hai điểm và . Nếu là trung điểm đoạn thẳng AB thì ; . |
b) Tọa độ trọng tâm tam giác
| Cho tam giác ABC có , , . Nếu là trọng tâm tam giác ABC thì ; . |
3. Biểu thức tọa độ của tích vô hướng
| Nếu và thì . |
Nhận xét:
a) Nếu thì .
b) Nếu và thì .
c) Với hai vecto và đều khác , ta có:
+ vuông góc khi và chỉ khi .
+ .
B. Bài tập
Bài 1: Cho , . Tìm tọa độ của và .
Giải:
; .
Bài 2: Cho ba điểm A(-1;-3), B(2;3) và C(3;5). Chứng minh ba điểm A, B, C thẳng hàng.
Giải:
Ta có: , . Suy ra .
Vậy ba điểm A, B, C thẳng hàng.
Bài 3: Cho tma giác ABC có A(-2;1), B(2;5), C(5;2). Tìm tọa độ trung điểm M của đoạn thẳng AB và trọng tâm G của tam giác ABC.
Giải:
Do là trung điểm của đoạn thẳng AB nên:
; .
Vậy M(0;3).
Do là trọng tâm tam giác ABC nên:
; .
Vậy .
Bài 4: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;2), B(1;-1), C(8;0).
a) Tính và .
b) Chứng minh .
c) Giải tam giác ABC.
Giải:
a) Ta có , . Do đó .
Mặt khác: , .
.
b) Do và nên .
Vậy .
c) Do nên , tức tam giác ABC vuông tại A.
Mà nên . Vì thế .
Mặt khác: , ,
.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365