Câu 1: (3,0 điểm) Thực hiện các phép tính sau:

a) $\frac{9}{4} + \frac{3}{4}:\left( {\frac{2}{3} - \frac{5}{9}} \right)$

b) $\frac{{{2^{15}}{{.9}^4}}}{{{6^6}{{.8}^3}}}$

c) $\sqrt {{{\left( { - 5} \right)}^2}}  - {\left( {{{2020}^0}} \right)^{2021}} - \left| { - \frac{1}{2}} \right|$

Câu 2: (2,0 điểm) Tìm x, biết:

a) $\frac{2}{3} - \left( {\frac{3}{4} + x} \right) = \sqrt {\frac{1}{9}}$

b) $\left| {x - \frac{3}{4}} \right| - 0,5 = 7$

Câu 3: (1,0 điểm) Hưởng ứng Hội thi vẽ tranh chủ đề “Thực hiện nếp sống văn minh đô thị, chung tay xây dựng đô thị thông minh” của Trung tâm Văn Hóa Quận 1, một trường Trung học cơ sở đã nhận được 216 bức tranh của bốn khối 6, 7, 8, 9. Biết rằng số bức tranh của các khối 6, 7, 8, 9 lần lượt tỉ lệ với 4; 6; 7; 10. Hỏi mỗi khối đã gửi tham gia hội thi bao nhiêu bức tranh vẽ?

Câu 4: (1,0 điểm) Theo ban chỉ đạo Tổng điều tra dân số và nhà ở năm 2019 Thành phố Hồ Chí Minh công bố, dân số của Thành phố Hồ Chí Minh năm 2019 là 8 993 082 người, tỉ lệ tăng dân số bình quân mỗi năm của Thành phố Hồ Chí Minh khoảng 2,28%.

a) Tính dân số của Thành phố Hồ Chí Minh vào năm 2020 (làm tròn đến chữ số hàng đơn vị)

b) Biết diện tích của Thành phố Hồ Chí Minh là 2095 km². Tính mật độ dân số (người/km²) ở Thành phố Hồ Chí Minh năm 2019 (làm tròn đến chữ số hàng đơn vị)

Mật độ dân số (người / km²) = Số lượng dân số ( người) : Diện tích lãnh thổ (km²)

Câu 5: (3,0 điểm) Cho tam giác ABC vuông tại A có $\widehat {ABC} = {60^0}$

a) Tính số đo góc BCA

b) Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE=BA.

Chứng minh $\Delta ADB = \Delta EDB$ và $DE \bot BC$.

c) Trên tia BA lấy điểm M sao cho BM = BC. Ba điểm E, D, M có thẳng hàng hay không? Giải thích câu trả lời của em.

LỜI GIẢI CHI TIẾT

Câu 1:

a)

 $\begin{array}{l}\frac{9}{4} + \frac{3}{4}:\left( {\frac{2}{3} - \frac{5}{9}} \right) = \frac{9}{4} + \frac{3}{4}:\left( {\frac{6}{9} - \frac{5}{9}} \right)\\ = \frac{9}{4} + \frac{3}{4}:\frac{1}{9} = \frac{9}{4} + \frac{{27}}{4}\\ = 4\end{array}$

b)

$\begin{array}{l}\frac{{{2^{15}}{{.9}^4}}}{{{6^6}{{.8}^3}}} = \frac{{{2^{15}}.{{\left( {{3^2}} \right)}^4}}}{{{{\left( {2.3} \right)}^6}.{{\left( {{2^3}} \right)}^3}}}\\ = \frac{{{2^{15}}{{.3}^8}}}{{{2^6}{{.3}^6}{{.2}^9}}} = \frac{{{2^{15}}{{.3}^8}}}{{{2^{15}}{{.3}^6}}}\\ = {3^2} = 9\end{array}$

c)

$\begin{array}{l}\sqrt {{{\left( { - 5} \right)}^2}}  - {\left( {{{2020}^0}} \right)^{2021}} - \left| { - \frac{1}{2}} \right|\\ = \sqrt {25}  - {1^{2021}} - \frac{1}{2}\\ = 5 - 1 - \frac{1}{2}\\ = 4 - \frac{1}{2}\\ = \frac{7}{2}\end{array}$

Câu 2:

a)

 $\begin{array}{l}\frac{2}{3} - \left( {\frac{3}{4} + x} \right) = \sqrt {\frac{1}{9}} \\ \Rightarrow \frac{2}{3} - \left( {\frac{3}{4} + x} \right) = \frac{1}{3}\\ \Rightarrow \frac{3}{4} + x = \frac{2}{3} - \frac{1}{3}\\ \Rightarrow \frac{3}{4} + x = \frac{1}{3}\\ \Rightarrow x = \frac{1}{3} - \frac{3}{4}\\ \Rightarrow x = \frac{{ - 5}}{{12}}\end{array}$

Vậy $x = \frac{{ - 5}}{{12}}$

b)

$\begin{array}{l}\left| {x - \frac{3}{4}} \right| - 0,5 = 7\\ \Rightarrow \left| {x - \frac{3}{4}} \right| - \frac{1}{2} = 7\\ \Rightarrow \left| {x - \frac{3}{4}} \right| = 7 + \frac{1}{2}\\ \Rightarrow \left| {x - \frac{3}{4}} \right| = \frac{{15}}{2}\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{x - \frac{3}{4} = \frac{{15}}{2}}\\{x - \frac{3}{4} =  - \frac{{15}}{2}}\end{array}} \right.\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{15}}{2} + \frac{3}{4}}\\{y = \frac{{ - 15}}{2} + \frac{3}{4}}\end{array}} \right.\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{33}}{4}}\\{x = \frac{{ - 27}}{4}}\end{array}} \right.\end{array}$

Vậy $x \in \left\{ {\frac{{33}}{4};\,\frac{{ - 27}}{4}} \right\}$

Câu 3:

Gọi số bức tranh vẽ các khối 6, 7, 8, 9 đã gửi tham gia hội thi lần lượt là x, y, z, t ($x,\,y,\,z,\,t \in {\mathbb{N}^*}$)

Do tổng số bức tranh của 4 khối đã gửi là 216 nên:

$x + y + z + t = 216\,\left( 1 \right)$

Do số bức tranh của các khối 6, 7, 8, 9 lần lượt tỉ lệ với 4; 6; 7; 10 nên:

$\frac{x}{4} = \frac{y}{6} = \frac{z}{7} = \frac{t}{{10}}\,\left( 2 \right)$

Từ (1) và (2) ta có: $\frac{x}{4} = \frac{y}{6} = \frac{z}{7} = \frac{t}{{10}}\,$ và $x + y + z + t = 216\,$

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{x}{4} = \frac{y}{6} = \frac{z}{7} = \frac{t}{{10}}\, = \frac{{x + y + z + t}}{{4 + 6 + 7 + 10}} = \frac{{216}}{{27}} = 8$

+) $\frac{x}{4} = 8 \Rightarrow x = 8.4 = 32$

+) $\frac{y}{6} = 8 \Rightarrow y = 8.6 = 48$

+) $\frac{z}{7} = 8 \Rightarrow z = 8.7 = 56$

+) $\frac{t}{{10}} = 8 \Rightarrow t = 8.10 = 80$

Vậy các khối 6, 7, 8, 9 đã gửi tham gia hội thi là: 32; 48; 56; 80 bức tranh.

Câu 4:

a) Từ năm 2019 đến năm 2020 dân số của Thành phố Hồ Chí Minh tăng là:

8 993 082 . 2,28:100 = 205 042 (người)

Dân số của Thành phố Hồ Chí Minh vào năm 2020 là:

8 993 082+ 205 042 = 9 918 124 (người)

Vậy dân số của Thành phố Hồ Chí Minh vào năm 2020 là 9 918 124 người

b) Mật độ dân số ở thành phố Hồ Chí Minh năm 2019 là:

8 993 082:2095 = 4293 (người / km²)

Câu 5:

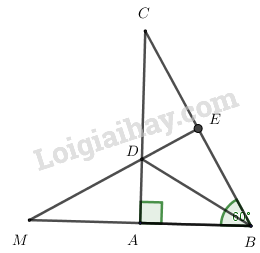
Xét tam giác ABC có:

$\begin{array}{l}\widehat {ABC} + \widehat {BAC} + \widehat {BCA} = {180^0}\\{60^0} + {90^0} + \widehat {BCA} = {180^0}\\\widehat {BCA} = {180^0} - {60^0} - {90^0}\\\widehat {BCA} = {30^0}\end{array}$

Vậy $\widehat {BCA} = {30^0}$.

b)

Xét $\Delta ADB$ và $\Delta EDB$ có:

BA=BE (gt)

$\widehat {EBD} = \widehat {ABD}$ (Do BD là phân giác của $\widehat {ABC}$ )

BD chung

$\Rightarrow \Delta ADB = \Delta EDB$ (c.g.c)

$\Rightarrow \widehat {DEB} = \widehat {DAB} = {90^0}$ (2 góc tương ứng)

Vậy $DE \bot BC$

c) E, D, M có thẳng hàng.

 Do BD là phân giác của $\widehat {ABC}$ nên:

 $\widehat {EBD} = \frac{{\widehat {ABC}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}$

Xét tam giác DEB vuông tại E nên:

$\widehat {EDB} = {90^0} - \widehat {DBE} = {90^0} - {30^0} = {60^0}$

$\Rightarrow \widehat {EDB} = \widehat {ADB} = {60^0}$ (2 góc tương ứng)

Ta có: BC=BM và BA=BE

 mà BC= BE+EC và BM= BA+AM

Suy ra EC=AM

Xét $\Delta EDC$ và $\Delta ADM$ có:

EC=AM

$\widehat {MAD} = \widehat {CED} = {90^0}$

AD=DE (do $\Delta ADB = \Delta EDB$)

$\Delta EDC = \Delta ADM$ (c.g.c)

$\Rightarrow \widehat {MDA} = \widehat {CDE}$(2 góc tương ứng) (3)

Mặt khác: Xét tam giác DCE vuông tại E có:

$\widehat {CDE} = {90^0} - {30^0} = {60^0}$ (4)

Từ (3) và (4) suy ra $\widehat {MAD} = {60^0}$

Ta có: $\widehat {EDB} + \widehat {ADB} + \widehat {ADM} = {60^0} + {60^0} + {60^0} = {180^0}$

Vậy E, D, M thẳng hàng.

baitap365.com