Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 2. Tính chất cơ bản của phân số
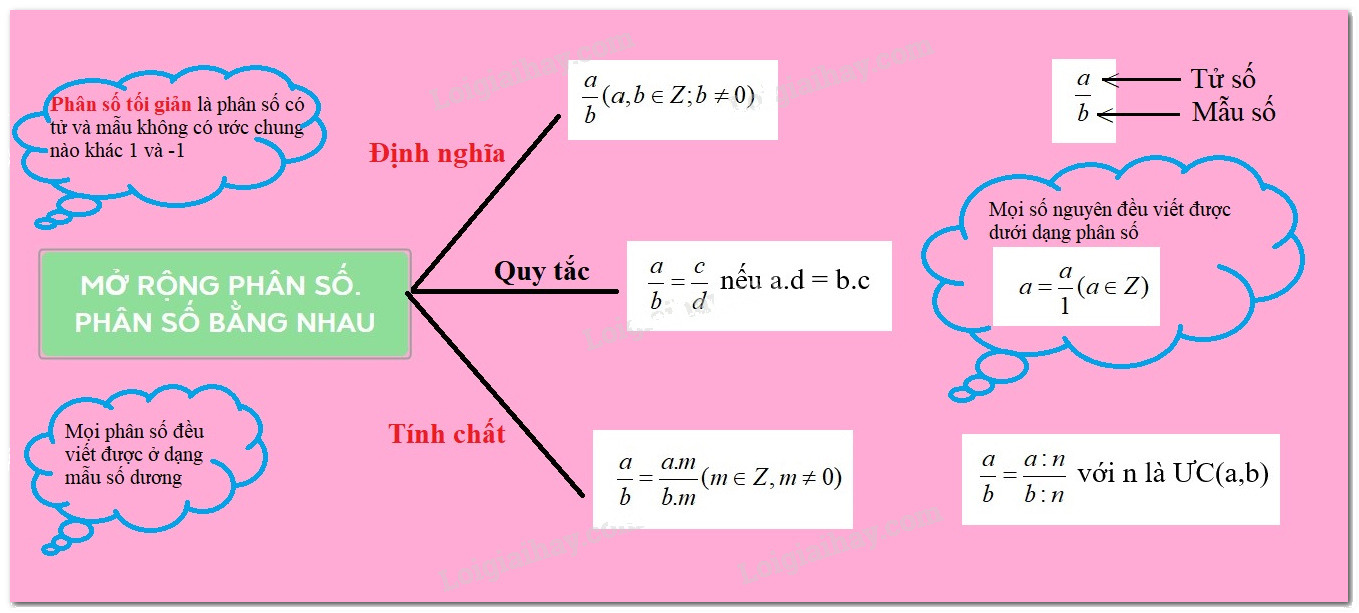
Lý thuyết Tính chất cơ bản của phân số
Trả lời hoạt động khám phá 1 trang 10 SGK Toán 6 Chân trời sáng tạo Trả lời hoạt động khám phá 2 trang 11 SGK Toán 6 Chân trời sáng tạo Trả lời thực hành 1 trang 11 SGK Toán 6 Chân trời sáng tạo Trả lời thực hành 2 trang 11 SGK Toán 6 Chân trời sáng tạo Giải bài 1 trang 12 SGK Toán 6 Chân trời sáng tạo Giải bài 2 trang 12 SGK Toán 6 Chân trời sáng tạo Giải bài 3 trang 12 SGK Toán 6 Chân trời sáng tạo tập 2 Giải bài 4 trang 12 SGK Toán 6 Chân trời sáng tạo Giải bài 5 trang 12 SGK Toán 6 Chân trời sáng tạo Giải bài 6 trang 12 SGK Toán 6 Chân trời sáng tạoLý thuyết Tính chất cơ bản của phân số
Lý thuyết Tính chất cơ bản của phân số Toán 6 Chân tời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.
ab=a.mb.mab=a.mb.m với m∈Zm∈Z và m≠0m≠0 .
Ví dụ:
a) 23=2.43.4=81223=2.43.4=812
b) −57=−5.27.2=−1014−57=−5.27.2=−1014
Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng ta được một phân số mới bằng phân số đã cho.
ab=a:nb:nab=a:nb:n với n∈n∈ƯC(a;b)(a;b).
Ví dụ:
a) 915=9:315:3=35915=9:315:3=35
b) −14−21=−14:7−21:7=23−14−21=−14:7−21:7=23
Bước 1: Viết các phân số đã cho về phân số có mẫu dương. Tìm BCNN của các mẫu dương đó để làm mẫu chung
Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu)
Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng.
Ví dụ:
Để quy đồng mẫu hai phân số 1616 và 3−83−8, ta làm như sau:
- Đưa về phân số có mẫu dương: 1616 và −38−38
- Tìm mẫu chung: BC(6;8)=24BC(6;8)=24
- Tìm thừa số phụ: 24:6=4;24:8=324:6=4;24:8=3
- Ta có: 16=1.46.4=42416=1.46.4=424 và 3−8=−38=−3.38.3=−9243−8=−38=−3.38.3=−924.
a) Khái niệm phân số tối giản:
Phân số tối giản là phân số mà tử và mẫu chỉ có ước chung là 11 và −1−1
b) Cách rút gọn phân số
Bước 1: Tìm ƯCLN của tử và mẫu khi đã bỏ dấu “-” (nếu có)
Bước 2: Chia cả tử và mẫu cho ƯCLN vừa tìm được, ta có phân số tối giản.
Ví dụ:
Để rút gọn phân số −1524−1524 ta làm như sau:
- Tìm ƯCLN của mẫu: ƯCLN(15; 24)=3.
- Chia cả tử và mẫu cho ƯCLN: −1524=−15:324:3=−58−1524=−15:324:3=−58.
Ta được −58−58 là phân số tối giản.
Áp dụng tính chất cơ bản của phân số
ab=a.mb.mab=a.mb.m với m∈Zm∈Z và m≠0m≠0; ab=a:nb:nab=a:nb:nvới n∈n∈ ƯC(a;b)(a;b).
Áp dụng tính chất cơ bản của phân số để biến đổi hai phân số đã cho thành hai phân số bằng chúng nhưng có từ (hoặc mẫu) như nhau. Khi đó mẫu (hoặc tử) của chúng phải bằng nhau. Từ đó tìm được số chưa biết.
Hoặc áp dụng định nghĩa hai phân số bằng nhau.
- Chia cả tử và mẫu của phân số abab cho ƯCLN của aa và bb để rút gọn thành phân số tối giản ( bỏ dấu “-” nếu có)
- Trường hợp biểu thức có dạng phân số, ta cần làm xuất hiện các thừa số chung của tử và mẫu rồi rút gọn các thừa số chung đó.
Để tìm phân số tối giản trong các phân số cho trước, ta tìm ƯCLN của tử và mẫu đối với từng phân số. Phân số nào có ƯCLN này là 11 thì đó là phân số tối giản.
Ví dụ:
Phân số −57−57 tối giản vì ƯCLN (5,7)=1.(5,7)=1.
Ta thực hiện hai bước:
- Rút gọn phân số đã cho đến tối giản, chằng hạn ta được phân số tối giản mnmn ;
- Dạng tổng quát của các phân số phải tìm là m.kn.km.kn.k (kk ∈∈ Z, k ≠0).
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365