Ví dụ: Cho ${z_1};{z_2}$ thỏa mãn $\left| {{z_1} - {z_2}} \right| = 1;\left| {{z_1} + {z_2}} \right| = 3.$ Tính max$T = \left| {{z_1}} \right| + \left| {{z_2}} \right|.$

A. $8$

B. $10$

C. $4$

D. $\sqrt {10}$

Giải

Đặt ${z_1} = {x_1} + {y_1}i;{z_2} = {x_2} + {y_2}i.$ $({x_1},{y_1},{x_2},{y_2} \in R)$. Điều kiện đã cho trở thành

+) $\left| {{z_1} - {z_2}} \right| = 1$$\Rightarrow \left| {{x_1} + {y_1}i - {x_2} - {y_2}i} \right| = 1 \Leftrightarrow \sqrt {{{({x_1} - {x_2})}^2} + {{({y_1} - {y_2})}^2}}  = 1$ 

$\Leftrightarrow {x_1}^2 + {x_2}^2 + {y_1}^2 + {y_2}^2 - 2{x_1}{x_2} - 2{y_1}{y_2} = 1$  (1)

+) $\left| {{z_1} + {z_2}} \right| = 3 \Rightarrow \left| {{x_1} + {y_1}i + {x_2} + {y_2}i} \right| = 3$

$\Leftrightarrow {x_1}^2 + {x_2}^2 + {y_1}^2 + {y_2}^2 + 2{x_1}{x_2} + 2{y_1}{y_2} = 9$  (2)

Cộng vế với vế của (1) và (2) ta được ${x_1}^2 + {x_2}^2 + {y_1}^2 + {y_2}^2 = 5$

+) $T = \left| {{z_1}} \right| + \left| {{z_2}} \right| = \sqrt {{x_1}^2 + {y_1}^2}  + \sqrt {{x_2}^2 + {y_2}^2}$

Áp dụng bất đẳng thức Bunhiacopxki ta được

$T = 1.\sqrt {{x_1}^2 + {y_1}^2}  + 1.\sqrt {{x_2}^2 + {y_2}^2}  \le \sqrt {\left( {1 + 1} \right).\left( {{x_1}^2 + {x_2}^2 + {y_1}^2 + {y_2}^2} \right)}$ 

$= \sqrt {2.5}  = \sqrt {10} \Rightarrow$ $\max T = \sqrt {10} .$

Đáp án D 

Ví dụ: Cho số phức $z = x + yi$ thỏa mãn $\left| {z - 2 - 4i} \right| = \left| {z - 2i} \right|$ đồng thời có mô đun nhỏ nhất. Tính $N = {x^2} + {y^2}.$

A. $N = 8$

B. $N = 10$

C. $N = 16$              

D. $N = 26$

Giải

Gọi $M(x,y)$ là điểm biểu diễn của số phức $z = x + yi$

+) $\left| {z - 2 - 4i} \right| = \left| {z - 2i} \right|$$\Rightarrow {(x - 2)^2} + {(y - 4)^2} = {x^2} + {(y - 2)^2} \Leftrightarrow  - 4x + 4 - 8y + 16 =  - 4y + 4$

$\Leftrightarrow 4x + 4y = 16 \Leftrightarrow x + y - 4 = 0$

Suy ra tập hợp điểm biểu diễn của $z$ là một đường thẳng $x + y - 4 = 0$

+) $N = {x^2} + {y^2} = {\left| z \right|^2}$

$\Rightarrow N$min$\Leftrightarrow \left| z \right|$min$\Leftrightarrow OM$min $\Rightarrow OM \bot d:x + y - 4 = 0$

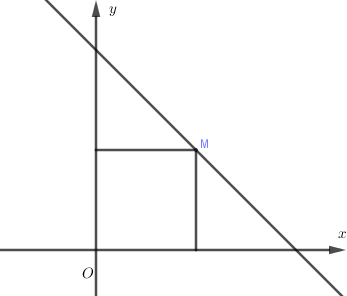
$\Rightarrow M(2,2)$  $\Rightarrow N = {2^2} + {2^2} = 8$

Đáp án A.

Ví dụ: Cho $z$ thỏa mãn $\left| {z - 2 - 4i} \right| = \sqrt 5 .$ Tìm max$\left| z \right|.$

A. $3\sqrt 5$

B. $5$

C. $\sqrt 5$                                     

D. $\sqrt {13}$

Giải

Dấu hiệu: Đề bài yêu cầu tính max của một mô đun ta sử dụng bất đẳng thức chứa dấu giá trị tuyệt đôi.

Ta có: $\left| z \right| - \left| { - 2 - 4i} \right| \le \left| {z - 2 - 4i} \right| \Leftrightarrow \left| z \right| - \sqrt {20}  \le \sqrt 5  \Leftrightarrow \left| z \right| \le \sqrt {20}  + \sqrt 5  = 3\sqrt 5$

$\Rightarrow$ max$\left| z \right| = 3\sqrt 5$

Đáp án A.