Các dạng toán về phương trình đường thẳng

1. Kiến thức cần nhớ

- Phương trình tham số của đường thẳng: $\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\left( {t \in \mathbb{R}} \right)$

ở đó $M\left( {{x_0};{y_0};{z_0}} \right)$ là điểm thuộc dường thẳng và $\overrightarrow u  = \left( {a;b;c} \right)$  là VTCP của đường thẳng.

- Phương trình chính tắc của đường thẳng: $\dfrac{{x - {x_0}}}{a} = \dfrac{{y - {y_0}}}{b} = \dfrac{{z - {z_0}}}{c}\left( {a,b,c \ne 0} \right)$

ở đó $M\left( {{x_0};{y_0};{z_0}} \right)$ là điểm thuộc dường thẳng và $\overrightarrow u  = \left( {a;b;c} \right)$  là VTCP của đường thẳng.

- Đườngthẳng $Ox:\left\{ \begin{array}{l}x = t\\y = 0\\z = 0\end{array} \right.\left( {t \in \mathbb{R}} \right);$ $Oy:\left\{ \begin{array}{l}x = 0\\y = t\\z = 0\end{array} \right.\left( {t \in \mathbb{R}} \right);$ $Oz:\left\{ \begin{array}{l}x = 0\\y = 0\\z = t\end{array} \right.\left( {t \in \mathbb{R}} \right)$

- Đường thẳng $AB$ có $\overrightarrow {{u_{AB}}}  = \overrightarrow {AB}$

- Đường thẳng ${d_1}//{d_2} \Rightarrow \overrightarrow {{u_1}}  = \overrightarrow {{u_2}}$

2. Một số dạng toán thường gặp

Dạng 3: Viết phương trình đường thẳng.

Phương pháp chung:

- Bước 1: Tìm điểm đi qua $A$.

- Bước 2: Tìm VTCP $\overrightarrow u$ của đường thẳng.

- Bước 3: Viết phương trình tham số hoặc chính tắc của đường thẳng biết hai yếu tố trên.

+) Đi qua hai điểm.

Đường thẳng $AB$ đi qua $A$ và nhận $\overrightarrow {AB}$ làm VTCP.

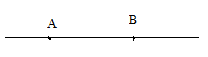
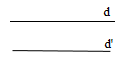
+) Đi qua một điểm và song song với một đường thẳng.

Đường thẳng $d$ qua $A$ và song song với $d'$ thì $d$ có VTCP $\overrightarrow {{u_d}}  = \overrightarrow {{u_{d'}}}$

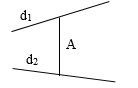
+) Đi qua một điểm và vuông góc với hai đường thẳng.

Đường thẳng $d$ đi qua điểm $A$ và vuông góc với hai đường thẳng ${d_1},{d_2}$ thì $d$ có VTCP $\overrightarrow u  = \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]$

3. Khoảng cách và góc 

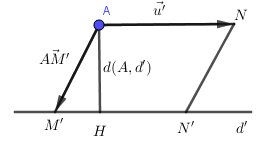
a) Khoảng cách từ điểm $A$ đến đường thẳng $d'$

b) Khoảng cách giữa hai đường thẳng:

c) Góc giữa hai đường thẳng có các VTCP lần lượt là: $\overrightarrow u ,\overrightarrow {u'}$: