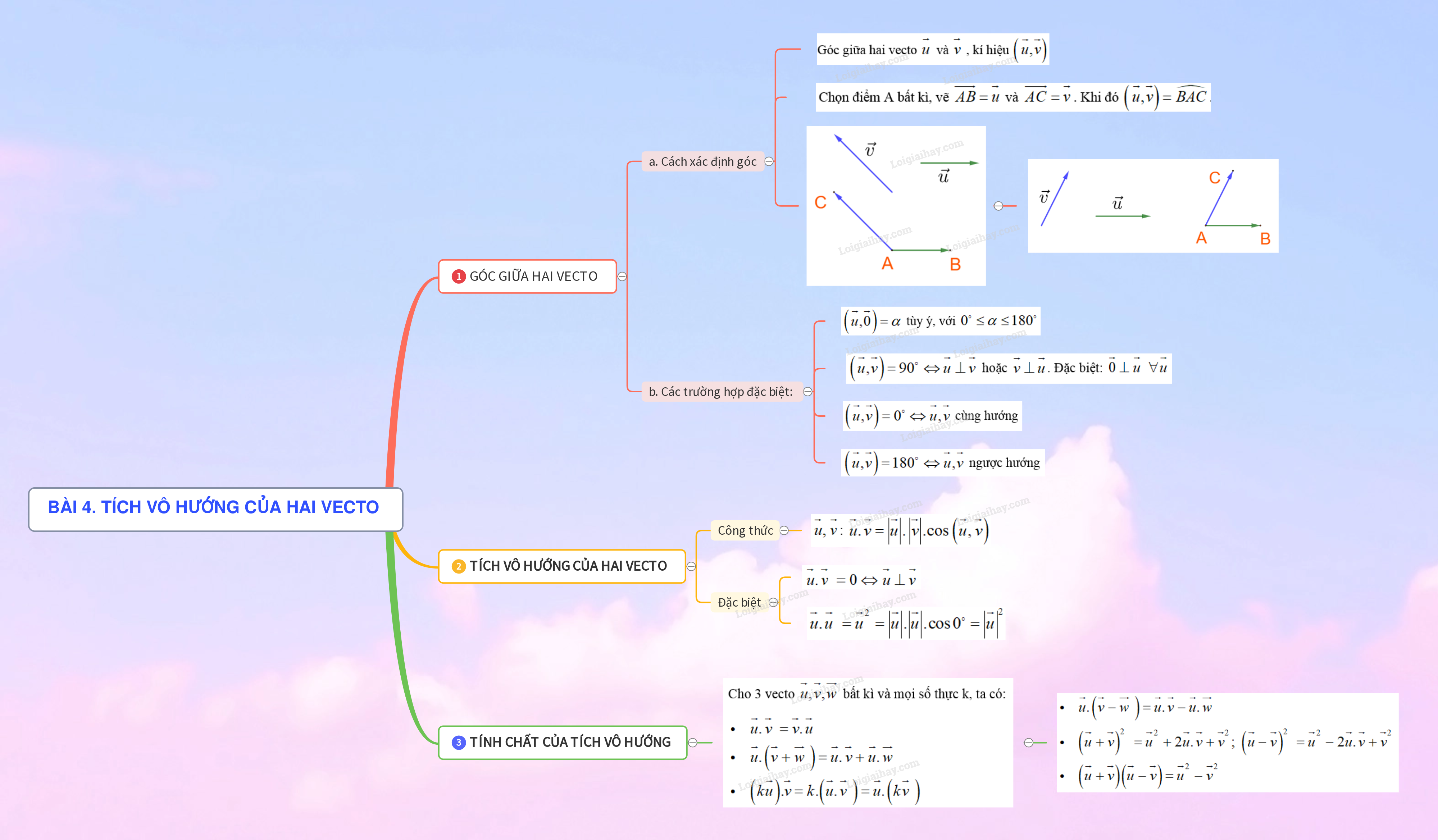
1. GÓC GIỮA HAI VECTO

Cho hai vecto $\overrightarrow u$ và $\overrightarrow v$ khác $\overrightarrow 0$. Góc giữa hai vecto $\overrightarrow u$ và $\overrightarrow v$ , kí hiệu $\left( {\;\overrightarrow u ,\overrightarrow v } \right)$

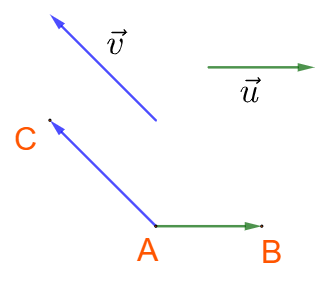
a) Cách xác định góc:

Chọn điểm A bất kì, vẽ $\overrightarrow {AB}  = \overrightarrow u$ và $\overrightarrow {AC}  = \overrightarrow v$. Khi đó $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}$.

b) Các trường hợp đặc biệt:

+) $\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha$ tùy ý, với ${0^ \circ } \le \alpha  \le {180^ \circ }$

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u  \bot \overrightarrow v$ hoặc $\overrightarrow v  \bot \overrightarrow u$. Đặc biệt: $\overrightarrow 0  \bot \overrightarrow u \;\;\forall \overrightarrow u \;$

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$ cùng hướng

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$ ngược hướng

2. TÍCH VÔ HƯỚNG CỦA HAI VECTO

+) Tích vô hướng của hai vecto $\overrightarrow u ,\;\overrightarrow v$: $\overrightarrow u .\;\overrightarrow v  = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)$

+) $\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u  \bot \;\overrightarrow v \;\;$

+) $\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}$

3. TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG

Cho 3 vecto $\overrightarrow u ,\overrightarrow v ,\overrightarrow w$ bất kì và mọi số thực k, ta có:

$\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v  + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v  = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}$

Hệ quả

$\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v  - \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; - \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u  + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u  - \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} - 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u  + \overrightarrow v } \right)\left( {\overrightarrow u  - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}$