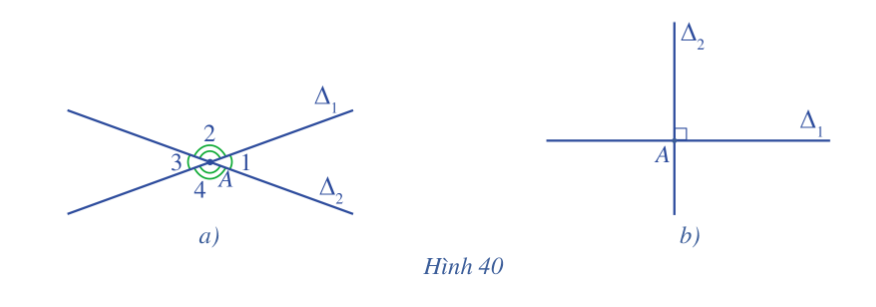
Trong mặt phẳng, cho hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ cắt nhau tại A tạo thành bốn góc  đỉnh A (quy ước không kể góc bẹt và góc không).

Quan sát Hình 40a và đọc tên một góc nhọn trong bốn góc đó.

Quan sát Hình 40b và nêu đặc điểm bốn góc tại đỉnh A.

Cho hai đường thẳng ${\Delta _1},{\Delta _2}$cắt nhau tại I và có vectơ chỉ phương lần lượt là $\overrightarrow {{u_1}} ,\overrightarrow {{u_2}}$. Gọi A và B là các điểm lần lượt thuộc hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ sao cho $\overrightarrow {{u_1}}  = \overrightarrow {IA} ,\overrightarrow {{u_2}}  = \overrightarrow {IB}$.

a) Quan sát Hình 41a, Hình 41b, hãy nhận xét về độ lớn của góc giữa hai đường thẳng

${\Delta _1},{\Delta _2}$và độ lớn của góc giữa hai vectơ $\overrightarrow {IA}$,$\overrightarrow {IB}$

b) Chứng tỏ cos(${\Delta _1},{\Delta _2}$) = $\left| {cos\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|$.

Trong mặt phẳng toạ độ, cho hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ có vectơ chỉ phương lần  lượt là$\overrightarrow {{u_1}}  = {\rm{ }}\left( {{a_1};{\rm{ }}{b_1}} \right),{\rm{ }}\overrightarrow {{u_2}} {\rm{ }} = {\rm{ }}\left( {{a_2};{b_2}} \right)$ . Tính $\cos \left( {{\Delta _1},{\Delta _2}} \right)$.

Tính số đo góc giữa hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ trong môi trường hợp sau:

a) ${\Delta _1}:\left\{ \begin{array}{l}x =  - 3 + 3\sqrt 3 t\\y = 2 + 3t\end{array} \right.$  và ${\Delta _2}:y - 4 = 0$

b)  ${\Delta _1}:2x - y = 0$ và ${\Delta _2}: - x + 3y - 5 = 0$