I. TRẮC NGHIỆM ( 2 điểm)

Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1. Nếu tam giác $ABC$ có trung tuyến $AM$ và $G$ là trọng tâm thì

A. $AG = GM$                      

B.$GM = \dfrac{1}{2}AG$      

C. $AG = \dfrac{1}{3}AM$     

D. $AM = 2.AG$

Câu 2: Trong biểu đồ hình quạt tròn, khẳng định nào sau đây không đúng?

     A. Hai hình quạt bằng nhau biểu diễn cùng một tỉ lệ.     

     B. Hình quạt nào lớn hơn biểu diễn số liệu lớn hơn.

     C. Cả hình tròn biểu diễn 75%.

     D. $\dfrac{1}{4}$ hình tròn biểu diễn 25%.                     

Câu 3. Cho $\Delta ABC,{\mkern 1mu} \hat A = {70^^\circ }$, hai đường phân giác BD và CE cắt nhau tại $O$, thế thì:

A. $\widehat {BOC} = {120^^\circ }$.                                

B. $\widehat {BAO} = \dfrac{1}{2}\widehat {BAC}$.          

C. $\widehat {BOC} = {160^^\circ }$.                                

D. $\widehat {BAO} < {30^^\circ }$.

Câu 4: Gọi $I$ là giao điểm của ba đường phân giác của tam giác thì:

A. $I$cách đều ba cạnh của tam giác.                            

B. $I$là trọng tâm của tam giác.                                     

C. $I$cách đều ba đỉnh của tam giác.                             

D. $I$ là trực tâm của tam giác.

Câu 5: Tính chất nào sau đây không phải của tam giác$ABC$cân tại $C$:

A. Trung tuyến $AM$và $BN$của tam giác $ABC$ bằng nhau.                              

B. $\angle A < {90^o}$.         

C. $AC > AB$.                       

D. $\angle A = \angle B$

Câu 6. Biểu đồ đoạn thẳng dưới đây cho biết lượng mưa trung bình trong 12 tháng tại Long An (đơn vị: mm).

Từ biểu đồ đoạn thẳng, hãy cho biết lượng mưa tăng trong những khoảng thời gian nào?

     A. Giữa các tháng 1 – 2; 6 – 7; 9 – 10; 10 – 11; 11 – 12.

     B. Giữa các tháng 2 – 3; 3 – 4; 4 – 5; 5 – 6; 7 – 8; 8 – 9.

     C. Giữa các tháng 1 – 6; 7 – 9.                                        

     D. Giữa các tháng 1 – 2; 6 – 7; 9 – 12.

Câu 7. Tập nghiệm của đa thức là:

1.                         B.                      C.                                  D.

Câu 8. Cho hai đa thức $f(x) =  - {x^5} + 2{x^4} - {x^2} - 1;g(x) =  - 6 + 2x - 3{x^3} - {x^4} + 3{x^5}$. Giá trị của $h(x) = f(x) - g(x)$ tại x = -1 là:

A. –8                          

B. –12                        

C. 10                          

D. 18

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1 (1,5 điểm)

Kết quả tìm hiểu về khả năng tự nấu ăn của tất cả học sinh lớp 7B cho bởi bảng thống kê sau:

a) Tính sĩ số lớp 7B.

b) Tính tỉ lệ % của những bạn có khả năng tự nấu ăn xuất sắc so với sĩ số lớp.

Bài 2. (3 điểm) Cho các đa thức:

$F\left( x \right) = 5{x^2} - 1 + 3x + {x^2} - 5{x^3}$ và $G\left( x \right) = 2 - 3{x^3} + 6{x^2} + 5x - 2{x^3} - x.$

a) Thu gọn và sắp xếp hai đa thức $F\left( x \right)$ và $G\left( x \right)$ theo lũy thừa giảm dần của biến.

b) Tính $M\left( x \right) = F\left( x \right) - G\left( x \right)$; Tìm nghiệm của đa thức $M\left( x \right)$

c) Tìm đa thức $N\left( x \right)$ biết $N\left( x \right) + F\left( x \right) =  - G\left( x \right)$

Bài 3. (3,5 điểm) Cho $\Delta ABC$cân tại $A$, tia phân giác của $\angle BAC$ cắt cạnh $BC$tại $D$. Kẻ $DH$vuông góc với $AB$tại $H$, kẻ $DK$vuông góc với $AC$tại $K$.

a) Chứng minh: $\Delta AHD = \Delta AKD$

b) Tia $KD$cắt tia $AB$tại $M$, tia $HD$cắt tia $AC$tại $N$. Chứng minh: $HM = KN$

c) Chứng minh: $AD \bot MN$và $BC//MN$

d) Gọi $I$là giao điểm của $AD$và $MN$. Qua $I$kẻ đường thẳng d song song với $AM$, đường thẳng $d$cắt $AN$tại $E$. Chứng minh: $IE = \dfrac{1}{2}AM$

Bài 4. (0,5 điểm) Cho đa thức $f\left( x \right)$ thỏa mãn $f\left( x \right) + x.f\left( { - x} \right) = x + 1$ với mọi giá trị của $x$. Tính $f\left( 1 \right)$.

I. Trắc nghiệm

Câu 1:

Phương pháp:

Nếu $\Delta ABC$ có trung tuyến $AM$ và trọng tâm $G$ thì $AG = \dfrac{2}{3}AM$.

Cách giải:

Nếu $\Delta ABC$ có trung tuyến $AM$ và trọng tâm $G$ thì $AG = \dfrac{2}{3}AM;GM = \dfrac{1}{3}AM;AG = 2GM$

Chọn B.

Câu 2:

Phương pháp:

Mô tả biểu đồ hình quạt tròn.

Cách giải:

Cả hình tròn biểu diễn 100% do đó, khẳng định “Cả hình tròn biểu diễn 75%” là không đúng.

Chọn C.

Câu 3:

Phương pháp: 

Sử dụng tính chất tia phân giác của góc và định lí tổng 3 góc trong một tam giác.

Cách giải:

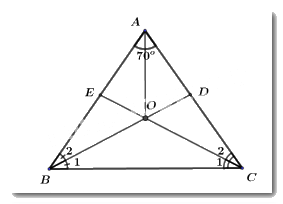
Ta có: $\widehat {BOC} = {180^^\circ }{\rm{ \;}} - \widehat {{B_1}} - \widehat {{C_1}}$.

Vì BD và CE lần lượt là các tia phân giác của góc B và C nên ta có: $\widehat {{B_1}} = \dfrac{{\hat B}}{2};{\mkern 1mu} \widehat {{C_1}} = \dfrac{{\hat C}}{2}$.

Trong tam giác ABC ta có: $\hat B + \hat C = {180^^\circ }{\rm{ \;}} - \hat A = {180^^\circ }{\rm{ \;}} - {70^^\circ }{\rm{ \;}} = {110^^\circ }$.

$\Rightarrow \widehat {BOC} = {180^^\circ }{\rm{ \;}} - \widehat {{B_1}} - \widehat {{C_1}} = {180^^\circ }{\rm{ \;}} - \dfrac{{\hat B + \hat C}}{2} = {180^^\circ }{\rm{ \;}} - {55^^\circ }{\rm{ \;}} = {125^^\circ }$

Chọn B.

Câu 4:

Phương pháp:

+ Mọi điểm nằm trên đường phân giác của một góc thì cách đều hai cạnh của góc.

+ Giao của ba đường phân giác trong tam giác cách đều ba cạnh của tam giác đó.

+ Giao điểm của ba đường phân giác trong tam giác là tâm đường tròn nội tiếp của tam giác đó.

Cách giải:

Gọi $I$ là giao điểm của ba đường phân giác của tam giác thì $I$cách đều ba cạnh của tam giác.

Chọn A.

Câu 5

Phương pháp:

+ Tam giác cân có hai góc ở đáy bằng nhau.

+ Tam giác cân có hai đường trung tuyến ứng với hai cạnh bên bằng nhau.

+ Tổng ba góc trong một tam giác bằng ${180^o}$

Cách giải:

+ Theo tính chất của tam giác cân thì A, D đúng.

+ Ta có $\angle A = \angle B = \dfrac{{{{180}^o} - \angle C}}{2} < {90^o}$ . Vậy B đúng.

+ Tam giác ABC cân tại C thì $AC > AB$hoặc $AC \le AB$. Vậy đáp án C sai.

Chọn C.

Câu 6.

Phương pháp:

Phân tích dữ liệu biểu đồ đoạn thẳng.

Cách giải:

Từ biểu đồ đoạn thẳng ta thấy lượng mưa tăng giữa các tháng 2 – 3; 3 – 4; 4 – 5; 5 – 6; 7 – 8; 8 – 9.        

Chọn B.

Câu 7.

Phương  pháp: Giải ${x^2} - 5x = 0$ để tìm nghiệm.

Hướng dẫn giải chi tiết

${x^2} - 5x = 0 \Rightarrow x(x - 5) = 0 \Rightarrow \left[ \begin{array}{l}x = 0\\x - 5 = 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = 0\\x = 5\end{array} \right.$

Vậy tập nghiệm của đa thức ${x^2} - 5x$là {0; 5}

Chọn C

Câu 8.

Phương  pháp:

-          Để trừ hai đa thức, ta nhóm các hạng tử cùng bậc với nhau và rút gọn.

-          Thay $x =  - 1$ vào đa thức h(x) vừa tìm được để tìm giá trị của h(x).

Cách giải:

$\begin{array}{l}h(x) = f(x) - g(x) = \left( { - {x^5} + 2{x^4} - {x^2} - 1} \right) - \left( { - 6 + 2x - 3{x^3} - {x^4} + 3{x^5}} \right)\,\,\,\\\;\;\;\;\;\;\; =  - {x^5} + 2{x^4} - {x^2} - 1 + 6 - 2x + 3{x^3} + {x^4} - 3{x^5}\\\;\;\;\;\;\;\; = \left( { - {x^5} - 3{x^5}} \right) + \left( {2{x^4} + {x^4}} \right) + 3{x^3} - {x^2} - 2x + 5\\\;\;\;\;\;\;\; =  - 4{x^5} + 3{x^4} + 3{x^3} - {x^2} - 2x + 5.\end{array}$

Thay $x =  - 1$ vào đa thức h(x) ta có: $h( - 1) =  - 4.{( - 1)^5} + 3.{( - 1)^4} + 3.{( - 1)^3} - {( - 1)^2} - 2.( - 1) + 5 =  - 4.( - 1) + 3.1 + 3.( - 1) - 1 + 2 + 5 = 10$

Vậy giá trị của h(x) là 10 tại $x =  - 1$.

Chọn C

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1.

Phương pháp:

Tỉ số phần trăm của a đối với b là: a : b . 100%

Cách giải

a) Sĩ số lớp 7B là:

18 +12 + 3 + 7 = 40 (học sinh).

b) Tỉ lệ phần trăm những bạn có khả năng tự nấu ăn xuất sắc so với sĩ số lớp là:

7 : 40.100 = 17,5

Bài 2.

Phương pháp

a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến của hai đa thức $F\left( x \right)$ và $G\left( x \right)$. Khi thu gọn các đơn thức đồng dạng ta cộng hệ số với nhau và giữ nguyên phần biến, sau đó sắp xếp theo lũy thừa giảm dần của biến số.

b) Tính $M\left( x \right) = F\left( x \right) - G\left( x \right)$. Ta thực hiện trừ hai đa thức. Sau đó tìm nghiệm của đa thức $M\left( x \right)$, ta cho $M\left( x \right) = 0$ để tìm nghiệm.

c) Biến đổi $N\left( x \right) + F\left( x \right) =  - G\left( x \right) \Rightarrow N\left( x \right) =  - F\left( x \right) - G\left( x \right)$, rồi thực hiện tính.

Chú ý: Trước dấu trừ các hạng tử đổi dấu.

Cách giải:

a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến.

Thu gọn $F\left( x \right):$

$\begin{array}{l}F\left( x \right) = 5{x^2} - 1 + 3x + {x^2} - 5{x^3}\\F\left( x \right) =  - 5{x^3} + \left( {5{x^2} + {x^2}} \right) + 3x - 1\\F\left( x \right) =  - 5{x^3} + 6{x^2} + 3x - 1\end{array}$

Thu gọn $G\left( x \right):$

$\begin{array}{l}G\left( x \right) = 2 - 3{x^3} + 6{x^2} + 5x - 2{x^3} - x.\\G\left( x \right) = \left( { - 3{x^3} - 2{x^3}} \right) + 6{x^2} + \left( {5x - x} \right) + 2\\G\left( x \right) =  - 5{x^3} + 6{x^2} + 4x + 2\end{array}$

b) Tính $M\left( x \right)$

$\begin{array}{l}M\left( x \right) = F\left( x \right) - G\left( x \right)\\M\left( x \right) = \left( { - 5{x^3} + 6{x^2} + 3x - 1} \right) - \left( { - 5{x^3} + 6{x^2} + 4x + 2} \right)\\M\left( x \right) =  - 5{x^3} + 6{x^2} + 3x - 1 + 5{x^3} - 6{x^2} - 4x - 2\\M\left( x \right) = \left( { - 5{x^3} + 5{x^3}} \right) + \left( {6{x^2} - 6{x^2}} \right) + \left( {3x - 4x} \right) + \left( { - 1 - 2} \right)\\M\left( x \right) = \,\, - x - 3\end{array}$

Tìm nghiệm của đa thức $M\left( x \right)$:

Ta có: $M\left( x \right) =  - x - 3 = 0 \Leftrightarrow x =  - 3$

Vậy $x =  - 3$ là nghiệm của đa thức $M\left( x \right)$.

c) Ta có:

$\begin{array}{l}N\left( x \right) + F\left( x \right) =  - G\left( x \right)\\ \Rightarrow N\left( x \right) =  - F\left( x \right) - G\left( x \right) =  - \left[ {F\left( x \right) + G\left( x \right)} \right]\end{array}$

Trong đó:

$F\left( x \right) =  - 5{x^3} + 6{x^2} + 3x - 1$

$G\left( x \right) =  - 5{x^3} + 6{x^2} + 4x + 2$

$\begin{array}{l} \Rightarrow F\left( x \right) + G\left( x \right)\\ = \left( { - 5{x^3} + 6{x^2} + 3x - 1} \right) + \left( { - 5{x^3} + 6{x^2} + 4x + 2} \right)\\ =  - 10{x^3} + 12{x^2} + 7x + 1\end{array}$

$\begin{array}{l} \Rightarrow N\left( x \right) =  - \left[ {F\left( x \right) + G\left( x \right)} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =  - \left( { - 10{x^3} + 12{x^2} + 7x + 1} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 10{x^3} - 12{x^2} - 7x - 1\end{array}$

Vậy $N\left( x \right) = 10{x^3} - 12{x^2} - 7x - 1$.

Câu 3:

Phương pháp:

+ Sử dụng các cách chứng minh hai tam giác bằng nhau.

+ Sử dụng tính chất của các góc tạo bởi một đường thẳng cắt hai đường thẳng song song.

+ Các định lí từ vuông góc tới song song.

+ Tính chất các đường cao, đường phân giác, đường trung trực trong tam giác cân.

Cách giải:

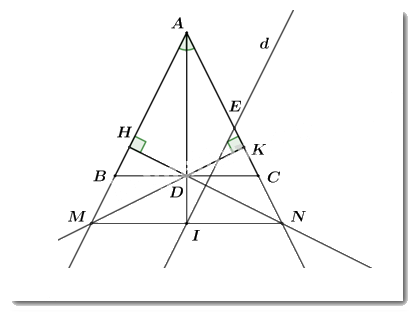
a) Xét hai tam giác vuông$\Delta AHD$và$\Delta AKD$có:

+ $AD$chung

+ $\angle HAD = \angle KAD$ (vì$AD$là tia phân giác của $\angle BAC$)

$\Rightarrow \Delta AHD =$$\Delta AKD$ (cạnh huyền – góc nhọn) (đpcm)

b) Theo a) $\Delta AHD =$$\Delta AKD$$\Rightarrow$$AH = AK$(hai cạnh tương ứng)    (1)

Xét hai tam giác vuông$\Delta AMK$và$\Delta ANH$có:

+ $\angle A$chung

+$AH = AK$

+ $\angle AKM = \angle AHN = {90^o}$

$\Rightarrow$$\Delta AMK = \Delta ANH$(g.c.g)

$\Rightarrow$$AM = AN$    (2)

Mà $\begin{array}{l}AM = AH + HM\\AN = AK + KN\end{array}$                                    (3)

Từ (1), (2), (3) suy ra $HM = KN$ (đpcm)

c) + Do $AM = AN$$\Rightarrow \Delta AMN$cân tại $A$

Vì $AD$là tia phân giác của góc $A$nên suy ra $AD$đồng thời là đường cao trong $\Delta AMN$ứng với cạnh $MN$.

$\Rightarrow AD \bot MN$ (đpcm).    (4)

+ $\Delta ABC$có $AD$là tia phân giác của góc $A$nên suy ra $AD$đồng thời là đường cao ứng với cạnh $BC$.

$\Rightarrow AD \bot BC$                               (5)

Từ (4), (5) suy ra $MN//BC$ (đpcm)

d) + Đường thẳng d song song với $AM$

$\Rightarrow$$\angle AMN = \angle EIN$(hai góc ở vị trí so le trong)                     (7)

Mặt khác $\Delta AMN$cân tại $A$$\Rightarrow$$\angle AMN = \angle ANM$                (8)

Từ (7) và (8) suy ra: $\angle EIN = \angle ANM = \angle ENI$

$\Rightarrow$$\Delta ENI$cân tại $E$

$\Rightarrow$$EI = EN$                                            (9)

+ Đường thẳng d song song với $AM$

$\Rightarrow$$\angle EIA = \angle MAI{\rm{     }}\left( { = \angle AIE} \right)$

$\Rightarrow$$\Delta EAI$cân tại $E$

$\Rightarrow$$EI = EA$                                            (10)

Từ (9) và (10) suy ra: $EI = EN = EA = \dfrac{1}{2}AN = \dfrac{1}{2}AM \Leftrightarrow EI = \dfrac{1}{2}AM$ (đpcm)

Bài 4.

Phương pháp:

Xét với $x =  - 1$, ta tìm được mối liên hệ của $f\left( { - 1} \right)$ và $f\left( 1 \right)$

Xét với $x = 1$, ta tìm được $f\left( 1 \right)$.

Cách giải:

+ Với $x =  - 1$, ta có: $f\left( { - 1} \right) + \left( { - 1} \right).f\left( 1 \right) =  - 1 + 1$

$\begin{array}{l} \Rightarrow f\left( { - 1} \right) - f\left( 1 \right) = 0\\ \Rightarrow f\left( { - 1} \right) = f\left( 1 \right)\end{array}$

+ Với $x = 1$, ta có: $f\left( 1 \right) + 1.f\left( { - 1} \right) = 1 + 1$

$\Rightarrow f\left( 1 \right) + f\left( { - 1} \right) = 2$

Suy ra, $f\left( 1 \right) + f\left( 1 \right) = 2$

$\begin{array}{l} \Rightarrow 2f\left( 1 \right) = 2\\ \Rightarrow f\left( 1 \right) = 1\end{array}$

Vậy $f\left( 1 \right) = 1$.