Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 7 Cánh diều
Đề thi giữa kì 2 Toán 7 - Đề số 4 - Cánh diều
Đề thi giữa kì 2 Toán 7 - Đề số 5 - Cánh diều Đề thi giữa kì 2 Toán 7 - Đề số 3 - Cánh diều Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 6 Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 7 Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 8 Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 9 Đề thi giữa kì 2 Toán 7 Cánh diều - Đề số 10 Đề thi giữa kì 2 Toán 7 - Đề số 2 - Cánh diều Đề thi giữa kì 2 Toán 7 - Đề số 1 - Cánh diềuĐề thi giữa kì 2 Toán 7 - Đề số 4 - Cánh diều
I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Một cửa hàng bán nước hoa quả đã khảo sát về các loại nước mà khách hàng ưa chuộng và thu được bảng dữ liệu sau:
|
Loại nước uống |
Nước cam |
Nước dứa |
Nước chanh |
Nước ổi |
|
Số người chọn |
12 |
8 |
17 |
10 |
Loại nước nào ít người ưa chuộng nhất?
A. Nước cam B. Nước dứa C. Nước chanh D. Nước ổi
Câu 2. Biểu thức đại số biểu thị bình phương của một tổng hai số a và b là:
A. a2−b2 B. a2+b2 C. (a−b)2 D. (a+b)2
Câu 3. Giá trị của biểu thức: x3−2x2 tại x=−2 là:
A. −16 B. 16 C. 0 D. −8
Câu 4. Biểu thức nào sau đây không là đơn thức?
A. 4x2y(−2x) B. 2x C. 2xy−x2 D. 2021
Câu 5. Sắp xếp các hạng tử của đa thức P(x)=2x3−7x2+x4−4 theo lũy thừa giảm dần của biến ta được:
A. P(x)=x4+2x3−7x2−4 B. P(x)=7x2+2x3+x4−4
C. P(x)=−4−7x2+2x3+x4 D. P(x)=x4−2x3−7x2−4
Câu 6. Cho tam giác MNP có NP=1cm,MP=7cm. Độ dài cạnh MN là một số nguyên (cm). Độ dài cạnh MN là:
A. 8cm B. 5cm C. 6cm D. 7cm
Câu 7. Cho tam giác ABC, có ∠A=900;∠C=300. Khi đó quan hệ giữa ba cạnh AB,AC,BC là:
A. BC>AB>AC B. AC>AB>BC C. AB>AC>BC D. BC>AC>AB
Câu 8. Giao điểm của 3 đường trung trực của tam giác
A. cách đều 3 cạnh của tam giác.
B. được gọi là trực tâm của tam giác.
C. cách đều 3 đỉnh của tam giác.
D. cách đỉnh một đoạn bằng 23 độ dài đường trung tuyến đi qua đỉnh đó.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Biểu đồ hình quạt tròn bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) lực lượng lao động (từ 15 tuổi trở lên) phân theo trình độ chuyên môn kĩ thuật (CMKT) của nước ta (năm 2020).
a) Trong năm 2020, có bao nhiêu phần trăm lực lượng lao động không có trình độ CMKT? Trình độ sơ cấp? Trình độ trung cấp? Trình độ cao đẳng? Trình độ đại học trở lên?
b) Trong năm 2020, lực lượng lao động không có trình độ CMKT gấp bao nhiêu lần lực lượng lao động có trình độ đại học trở lên (làm tròn đến hàng đơn vị)?
c) Số lao động có trình độ đại học trở lên năm 2020 là bao nhiêu triệu người, biết có 54,6 triệu người từ 15 tuổi trở lên thuộc lực lượng lao động của cả nước trong năm 2020 (làm tròn kết quả đến hàng phần trăm)?
Bài 3. (2 điểm) Cho hai đa thức: f(x)=x5+x3−4x−x5+3x+7 và g(x)=3x2−x3+8x−3x2−14.
a) Thu gọn và sắp xếp hai đa thức f(x) và g(x) theo lũy thừa giảm dần của biến.
b) Tính f(x)+g(x) và tìm nghiệm của đa thức f(x)+g(x).
Bài 4. (3,5 điểm) Cho tam giác ABC cân tại A, kẻ AHvuông góc với BC(H∈BC). Gọi P là trung điểm của HC. Trên tia đối của tia PA lấy điểm Q sao cho QP=PA.
a) Chứng minh rằng: ΔAPH=ΔQPC và QC vuông góc vớiBC.
b) Chứng minh rằng: QC=AHtừ đó suy ra AC>QC.
c) Chứng minh rằng: ∠PAC<∠HAP
d) Gọi I là trung điểm của BQ. Chứng minh rằng ba điểm A,H,I thẳng hàng.
Bài 5. (0,5 điểm) Cho các số thực a,b,c,d,e thỏa mãn: ab=bc=cd=de.
Chứng minh rằng: (2019b+2020c−2021d2019c+2020d−2021e)3=a2bc.
(Giả thiết các tỉ số đều có nghĩa)
Lời giải
I. Trắc nghiệm
|
1.B |
2. D |
3. A |
4. C |
|
5. A |
6. D |
7. D |
8. C |
Câu 1.
Phương pháp:
Đọc và miêu tả dữ liệu từ bảng thống kê.
Cách giải:
Loại nước ít người ưa chuộng nhất là nước dứa.
Chọn B.
Câu 2.
Phương pháp:
Dùng các chữ, các số và các phép toán để diễn đạt các mệnh đề phát biểu bằng lời.
Cách giải:
Bình phương của một tổng hai số a và b là: (a+b)2
Chọn D.
Câu 3.
Phương pháp:
Thay x=−2 vào biểu thức x3−2x2 để tính.
Cách giải:
Thay x=−2 vào biểu thức x3−2x2 ta có: (−2)3−2.(−2)2=(−8)−2.4=−16
Chọn A.
Câu 4.
Phương pháp:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức: 2xy−x2 không là một đơn thức.
Chọn C.
Câu 5.
Phương pháp:
Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
Cách giải:
Sắp xếp theo lũy thừa giảm dần của biến: P(x)=x4+2x3−7x2−4
Chọn A.
Câu 6.
Phương pháp:
Sử dụng hệ quả của bất đẳng thức trong tam giác:
+ Tồn tại một tam giác có độ dài ba cạnh là a,b,c nếu |b−c|<a<b+c.
+ Trong trường hợp xác định được a là số lớn nhất trong ba số a,b,c thì điều kiện tồn tại tam giác là a<b+c.
Cách giải:
Xét tam giác MNP, ta có:
|NP−MP|<MN<NP+MP⇒|1−7|<MN<1+7⇒6<MN<8
Vì độ dài cạnh MN là một số nguyên nên MN=7(cm)
Chọn D.
Câu 7.
Phương pháp:
Sử dụng quan hệ giữa góc và cạnh đối diện trong tam giác.
Cách giải:
Xét ΔABC có: ∠A+∠B+∠C=1800 (định lý tổng ba góc trong một tam giác)
⇒900+∠B+300=1800⇒∠B+1200=1800⇒∠B=600
Ta có: ∠C<∠B<∠A (vì 300<600<900)
⇒AB<AC<BC (quan hệ giữa góc và cạnh đối diện trong tam giác)
Chọn D.
Câu 8.
Phương pháp
Tính chất đồng quy của 3 đường trung trực của tam giác
Lời giải
3 đường trung trực của tam giác đồng quy tại 1 điểm, điểm này cách đều 3 đỉnh của tam giác.
Chọn C.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Phương pháp:
a) Đọc và mô tả biểu đồ hình quạt tròn.
b) Thực hiện phép chia.
c) Số lao động có trình độ đại học trở lên năm 2020 = % tương ứng . số người lao động.
Cách giải:
a) Trong năm 2020, có:
+ 76% lực lượng lao động không có trình độ CMKT;
+ 4,7% lực lượng lao động có trình độ sơ cấp;
+ 4,4 % lực lượng lao động có trình độ trung cấp;
+ 3,8% lực lượng lao động có trình độ cao đẳng;
+ 11,1% lực lượng lao động có trình độ đại học trở lên.
b) Từ biểu đồ hình quạt tròn, ta thấy 76% lực lượng lao động không có trình độ CMKT; 11,1% lực lượng lao động có trình độ đại học trở lên.
Ta có: 76%:11,1%=76100:11,1100=76100.10011,1=7611,1=6,(846)≈7
Vậy lực lượng lao động không có trình độ CMKT gấp 7 lần lực lượng lao động có trình độ đại học trở lên.
c) Số lao động có trình độ đại học trở lên năm 2020 là: 11,1%.54,6=11,1100.54610=6,0606≈6,06 (triệu người)
Bài 2.
Phương pháp:
a) Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
b) Tính f(x)+g(x) ta nhóm các hạng tử đồng dạng lại rồi thu gọn chúng.
Tìm nghiệm của đa thức f(x)+g(x), ta giải phương trình f(x)+g(x)=0
Cách giải:
a) f(x)=x5+x3−4x−x5+3x+7
f(x)=(x5−x5)+x3+(−4x+3x)+7f(x)=x3−x+7
g(x)=3x2−x3+8x−3x2−14g(x)=−x3+(3x2−3x2)+8x−14g(x)=−x3+8x−14
b) f(x)+g(x)=x3−x+7−x3+8x−14
=x3−x+7−x3+8x−14=(x3−x3)+(−x+8x)+(7−14)=7x−7
Ta có: f(x)+g(x)=0
7x−7=07x=7x=1
Vậy x=1 là nghiệm của đa thức f(x)+g(x)
Bài 3.
Phương pháp:
+ Sử dụng các cách chứng minh hai tam giác bằng nhau.
+ Mối quan hệ giữa góc và cạnh trong tam giác (Cạnh đối diện với góc lớn hơn thì lớn hơn)
+ Tính chất trọng tâm của tam giác.
Cách giải:
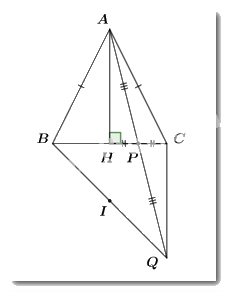
a. Xét ΔAPHvà ΔQPCcó:
+ HP=PC(gt)
+ ∠APH=∠QPC(đối đỉnh)
+ QP=PA (gt)
⇒ΔAPH=ΔQPC (c.g.c) (đpcm).
⇒∠AHP=∠QCP=90o(hai góc tương ứng)
⇒QC⊥BC(đpcm).
b. Theo (a) ΔAPH=ΔQPC
⇒QC=AH(hai cạnh tương ứng) (1)
Mà ΔAHCvuông tại H ⇒AH<AC(cạnh góc vuông <cạnh huyền) (2)
Từ (1) và (2), suy ra QC<AC(đpcm).
c. Xét ΔAQCcó QC<AC⇒∠QAC<∠AQC (3) (Mối quan hệ giữa cạnh- góc trong tam giác)
Mặt khác ΔAPH=ΔQPC⇒∠HAP=∠PQC=∠AQC (4)
Từ (3) và (4) ⇒∠HAP<∠QAC hay ∠HAP<∠PAC(đpcm).
d. Xét ΔABQcó BPlà trung tuyến ứng với cạnh AQ
Mà BH=2HP(do H là trung điểm của BC, Plà trung điểm của HC) ⇒Hlà trọng tâm ΔABQ (5)
Lại có Ilà trung điểm của BQ ⇒AIlà trung tuyến ứng với cạnh BQ (6)
Từ (5), (6) ⇒H∈AI
⇒A,H,Ithẳng hàng (đpcm)
Bài 4.
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Ta có: ab=bc=cd=de nên ab=2019b2019c=2020c2020d=2021d2021e
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: 2019b2019c=2020c2020d=2021d2021e=2019b+2020c−2021d2019c+2020d−2021e
Mà ab=2019b2020c và ab=bc (gt) nên (2019b+2020c−2021d2019c+2020d−2021e)3=(ab)3=a2b2.ab=a2b2.bc=a2bc (đpcm)
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365