Xét hàm số $f\left( x \right) = 2x.$

a) Xét dãy số $\left( {{x_n}} \right),$ với ${x_n} = 1 + \frac{1}{n}.$ Hoàn thành bảng giá trị $f\left( {{x_n}} \right)$ tương ứng.

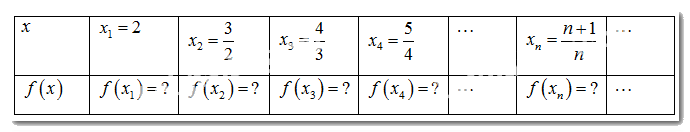
Các giá trị tương ứng của hàm số $f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),...$ lập thành một dãy số mà ta kí hiệu là $\left( {f\left( {{x_n}} \right)} \right).$ Tìm $\lim f\left( {{x_n}} \right).$

b) Chứng minh rằng với dãy số bất kì $\left( {{x_n}} \right),{x_n} \to 1$ ta luôn có $f\left( {{x_n}} \right) \to 2.$

Sử dụng định nghĩa, chứng minh rằng $\mathop {\lim }\limits_{x \to 2} {x^2} = 4.$

Cho hai hàm số $f\left( x \right) = {x^2} - 1,g\left( x \right) = x + 1.$

a) Tính $\mathop {\lim }\limits_{x \to 1} f\left( x \right)$ và $\mathop {\lim }\limits_{x \to 1} g\left( x \right).$

b) Tính $\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]$và so sánh $\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).$

c) Tính $\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right]$và so sánh $\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).$

d) Tính $\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right]$và so sánh $\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).$

e) Tính $\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}}$và so sánh $\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.$

Tính:

a) $\mathop {\lim }\limits_{x \to 2} \left[ {\left( {x + 1} \right)\left( {{x^2} + 2x} \right)} \right];$                         

b) $\mathop {\lim }\limits_{x \to 2} \sqrt {{x^2} + x + 3} .$

Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l} - 1,\,\,x < 0\\0,\,\,x = 0\\1,\,\,x > 0\end{array} \right.$

Hàm số $f\left( x \right)$ có đồ thị ở Hình 6.

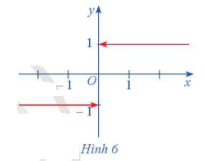
a) Xét dãy số $\left( {{u_n}} \right)$ sao cho ${u_n} < 0$ và $\lim {u_n} = 0.$ Xác định $f\left( {{u_n}} \right)$ và tìm $\lim f\left( {{u_n}} \right).$

b) Xét dãy số $\left( {{v_n}} \right)$ sao cho ${v_n} > 0$ và $\lim {v_n} = 0.$ Xác định $f\left( {{v_n}} \right)$ và tìm $\lim f\left( {{v_n}} \right).$

Tính $\mathop {\lim }\limits_{x \to  - {4^ + }} \left( {\sqrt {x + 4}  + x} \right)$