1. Hệ số góc của đường thẳng

Góc tạo bởi đường thẳng y = ax + b (a$\ne$0) và trục Ox.

Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a$\ne$0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.

Góc $\alpha$ tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc $\alpha$)

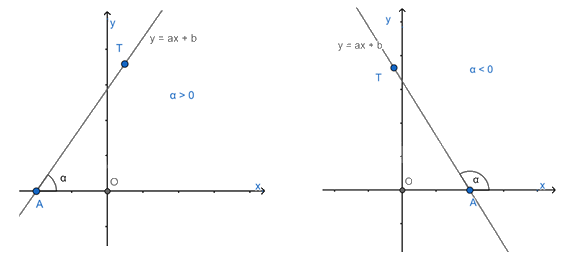
Hệ số góc: Ta gọi a là hệ số góc của đường thẳng y = ax + b (a$\ne$0).

Ví dụ: Đường thẳng y = 3x – 1 có hệ số góc là 3;

y = 2 – x có hệ số góc là -1.

2. Hai đường thẳng song song, hai đường thẳng cắt nhau

Hai đường thẳng y = ax + b (a$\ne$0) và y = a’x + b’ (a’$\ne$0) song song với nhau khi a = a’; b $\ne$ b’ và ngược lại.

Hai đường thẳng y = ax + b (a$\ne$0) và y = a’x + b’ (a’$\ne$0) trùng nhau khi a = a’; b = b’ và ngược lại.

Hai đường thẳng y = ax + b (a$\ne$0) và y = a’x + b’ (a’$\ne$0) cắt nhau khi a $\ne$ a’ và ngược lại.

Ví dụ: Đường thẳng y = -x + 1 và đường thẳng y = -x song song với nhau.

Đường thẳng y = -x + 1 và đường thẳng y = 2x + 1 cắt nhau.