Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com

Bài 3. Hàm số mũ. Hàm số lôgarit Toán 11 Chân trời sáng tạo
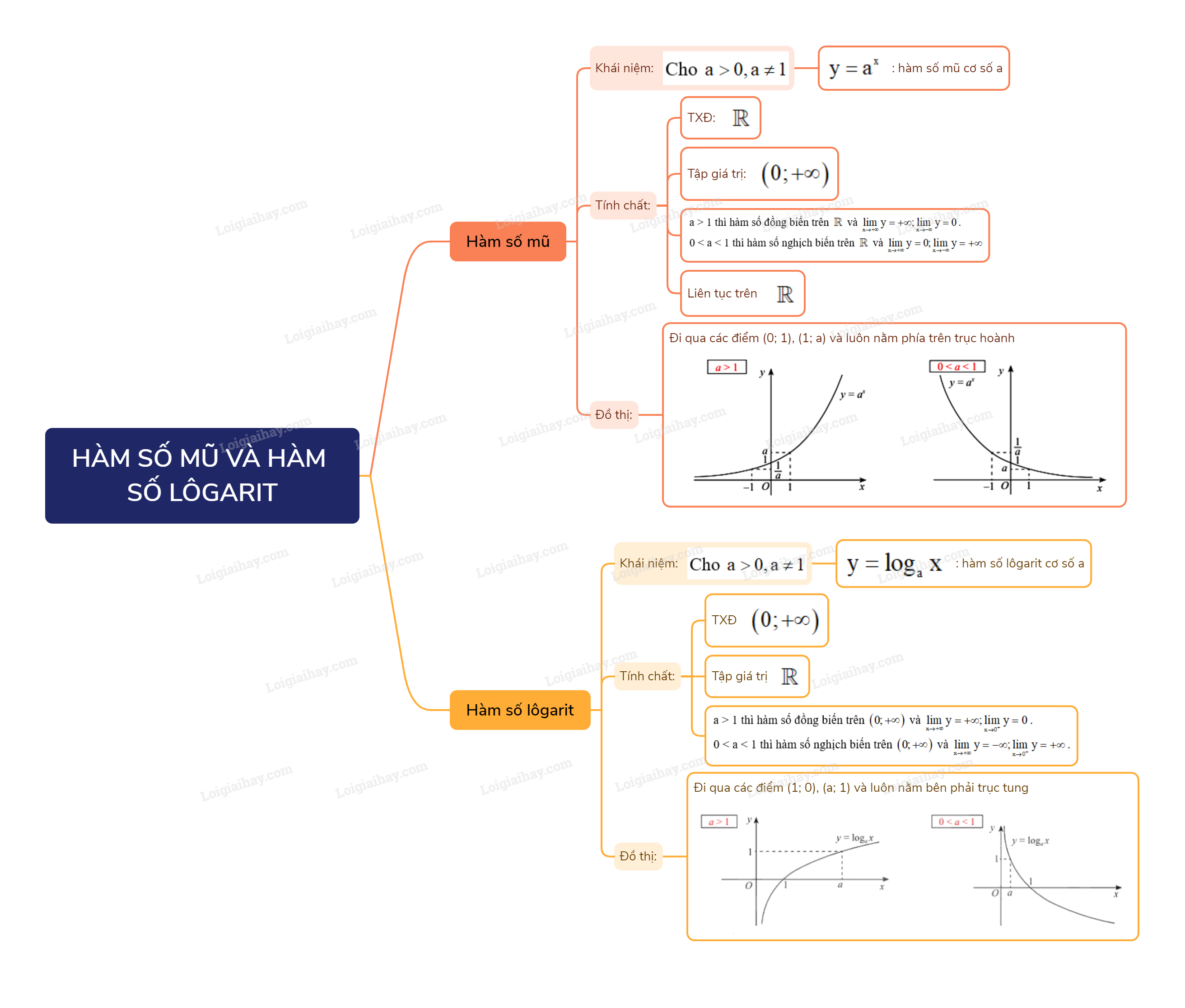
Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo
Giải mục 1 trang 19, 20, 21, 22 SGK Toán 11 tập 2 - Chân trời sáng tạo Giải mục 2 trang 22, 23, 24 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 1 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 2 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 3 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 4 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 5 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 6 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 7 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạoLý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo
1. Hàm số mũ - Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.
1. Hàm số mũ
- Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.
- Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có:
+ Tập xác định: \(D = \mathbb{R}\).
+ Tập giá trị: \(T = \left( {0; + \infty } \right)\).
+ Hàm số liên tục trên \(\mathbb{R}\).
+ Sự biến thiên:
+ Đồ thị:
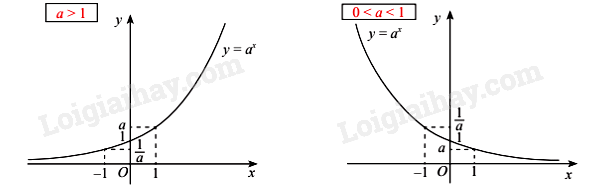
2. Hàm số lôgarit
- Hàm số \(y = {\log _a}x\left( {a > 0;a \ne 1} \right)\) được gọi là hàm số lôgarit cơ số a.
- Hàm số \(y = {\log _a}x\left( {a > 0;a \ne 1} \right)\) có:
+ Tập xác định: \(D = \left( {0; + \infty } \right)\).
+ Tập giá trị: \(T = \mathbb{R}\).
+ Hàm số liên tục trên \(\left( {0; + \infty } \right)\).
+ Sự biến thiên:
+ Đồ thị:
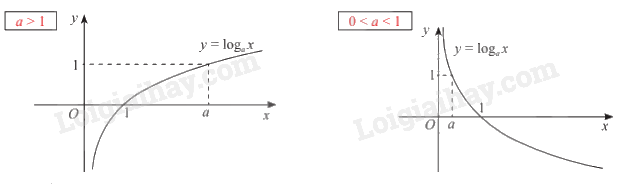
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365